Для преодоления отмеченного несоответствия при проведении финансового мониторинга доходность, ликвидность и риски банка следует определять в результате оценки (измерения) искомых показателей с помощью соответствующих бизнес-моделей. В частности, для оценки доходности банка требуется применение модели формирования доходов и расходов по финансовым инструментам.
Модель формирования доходов и расходов по финансовым инструментам может базироваться на данных бухгалтерского учета или на данных аналитического учета сделок, совершаемых банком. В первом случае основные трудности связаны с построением схемы движения средств, влияющих на финансовый результат, по счетам бухгалтерского учета и с расчетом корректировок по методу начисления. Сложности во втором случае обусловлены необходимостью разработки совершенной системы классификации финансовых инструментов в разрезе видов сделок и надежной методики выделения финансового результата и консолидации большого объема неоднородной информации по всем категориям финансовых инструментов.
Вне зависимости от выбранной модели формирования доходов и расходов по финансовым инструментам в процессе ее реализации придется опираться на мотивированное суждение, сформулированное банковскими специалистами. Кроме того, в ряде случаев классификация по финансовым инструментам неоднозначна с точки зрения финансового, управленческого и налогового учета. Как следствие этого, полученная оценка доходности будет содержать какой-то элемент субъективизма. Например, из-за того, что репортные, лизинговые, факторинговые и форфейтинговые сделки допускают неоднозначную экономическую интерпретацию, полученный по ним финансовый результат может оцениваться по-разному.
Мониторинг ликвидности является одной из составляющих системы управления ликвидностью банка, основную задачу которой можно сформулировать как поддержание достаточного уровня ликвидности и платежеспособности банка. Основные аспекты в состоянии активов и пассивов, которые должна учитывать модель, демонстрирующая изменения в ликвидности, – распределение по срокам погашения и динамика их отдельных категорий. Пример модели, демонстрирующей изменения в ликвидности банка, представлен на рис. 3.1. В деятельности банка, как правило, существуют сделки, находящиеся на разных стадиях реализации, – планируемые, срочные, незавершенные, – о которых известно, что в некоторый момент в будущем по ним могут возникнуть требования (или обязательства), и, учитывая эти аспекты будущего изменения ликвидности, возможно получение не только статических, но и динамических характеристик ликвидности.
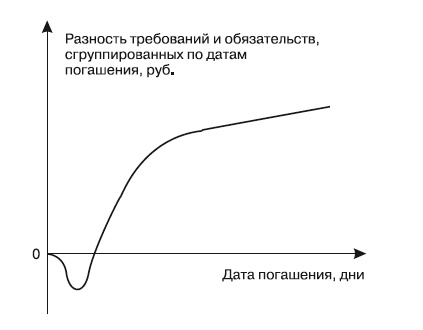
Рис. 3.1. Пример модели ликвидности банка
Текущая деятельность банка, как и любой коммерческой организации, сопряжена с риском, и как характеристика деятельности этот показатель имеет стратегическую значимость. Управление рисками – важная составляющая финансового менеджмента. Вместе с тем нет не только общепризнанного взаимоприемлемого определения термина «риск», но и отсутствует единая точка зрения на содержание самого понятия риска, поэтому на практике специалисты применяют разнообразные существенно различающиеся между собой трактовки и подходы к оценке риска.
Риск сопутствует деятельности хозяйствующего субъекта на протяжении всего периода его деловой активности и обычно определяется как опасность, возможность убытка или ущерба. Риск расценивается как негативное явление, которое следует если не исключить полностью, то по возможности ограничить. В общем виде комплексный контроль рисков в той или иной форме включает в себя исследование проблемной области, идентификацию, систематизацию, анализ, количественную оценку и управление рисками.
Природа рисков непосредственно связана с неопределенностью исхода, обусловленной неточностью, неполнотой и недостоверностью сведений о возможных событиях. Следовательно, уменьшение неопределенности любым возможным способом обычно приводит к снижению риска. При всей многогранности понятия риска следует выделить три его основных аспекта:
✓ риск предполагает возможность какого-то события;
✓ если событие произойдет, то оно повлечет за собой существенные последствия;
✓ в той или иной форме, как правило, проявляется «человеческий фактор».
Риск с учетом присущих ему особенностей можно определить как ситуативную характеристику деятельности, отражающую неопределенность ее исхода и возможность наступления неблагоприятных последствий. Приведенное определение, не являясь исчерпывающим и совершенным, все же отражает перечисленные аспекты риска.
Оценка рисков имеет большое прикладное значение и является составной частью правил оценки достаточности капитала, установленных новым Соглашением, разработанным Базельским комитетом по банковскому надзору (Базель II). Одной из целей Соглашения Базель II является распространение практики управления банковскими рисками, а также разработка требований к обеспечению надежности применяемых количественных показателей и моделей риска.
Для формализованного описания и оценки рисков банковской деятельности, источником которых является неопределенность финансовых результатов, традиционно используются методы прикладной статистики. В связи с тем что для построения математических моделей банковских рисков могут применяться прямые и косвенные статистические методы, вероятностные модели рисков имеет смысл разделять по этому признаку на модели первого и второго рода.
Вероятностные модели первого рода оперируют оценками вероятности некоторого случайного события P(^) или случайной величины P(X), при этом для их построения применяются различные параметрические и непараметрические методы прикладной статистики. Типичным примером события, вероятность которого может оцениваться посредством модели риска, является банкротство организации. К числу вероятностных моделей, в основе которых лежит применение случайных величин, относится группа моделей оценки стоимости, подверженной риску (Value-at-Risk – VAR). Если последствия реализации риска не носят катастрофический характер и размер связанного с ними ущерба равен Q, то стоимость риска С в рамках вероятностной математической модели применительно к случайному событию A и случайной величине X соответственно удовлетворяет выражениям:
C(A) = P(A) × Q(A);
C ≥ p(X) × Q(X) × dx,
где p(X) – плотность распределения случайной величины X;
Q(X) – размер ущерба как функция случайной величины X.
Вероятность комбинации нескольких случайных событий описывается формулой полной вероятности, в частном случае комбинации двух событий А и В, имеющей вид:
P(A, B) = P(A|B) × P(B) = P(B|A) × P(A).
Сравнивая математические модели риска, оперирующие оценками вероятности некоторого события P(A) или величины P(X), следует отметить, что при прочих равных условиях модели второй группы содержат большее число параметров, сложнее с точки зрения формирования, анализа и применения и при этом являются более информативными. Главным достоинством вероятностных моделей первого рода является возможность при их использовании опираться на весь арсенал доступных методов прикладной статистики.



