При использовании метода VA ситуация усложняется. С одной стороны, рост VA-цели становится несущественным на долгом отрезке времени, так как скорость роста рынка ее опережает. С другой стороны, часть накопленных средств периодически продается, общая сумма сбережений со временем уменьшается.
Одним из возможных способов преодоления этой проблемы является регулярное увеличение VA-цели на уровень инфляции. Например, при «классическом» подходе мы планировали увеличивать нашу VA-цель на $1 в месяц. Допустим, на нашем счету находится $100. При этом инфляция составляет 0,5 % в месяц. Согласно нашему модифицированному способу, мы будем рассчитывать VA-цель следующим образом. Сначала мы увеличим $1 на 0,5 % и получим $1,005. Затем мы увеличим $100 на 0,5 % и получим $100,05. После этого полученный результат увеличим на уровень инфляции ($100,05 + $1,005) × 1,005 = $101,56. С помощью аналогичного похода VA-цель последующего месяца рассчитывается как ($101,56+$1,005) × 1,005 = $103,08. При использовании «классического» VA-метода VA-цель второго месяца составила бы только $102. Налицо эффект компаундинга
[1]. Результаты методов DCA и VA, модифицированных по этой схеме, сравниваются во второй строчке таблицы на рис. 5.3. Уровень среднегодовой доходности метода VA при таких параметрах приближается к уровню DCA, но все равно остается ниже. Причина этого заключается в том, что уровень роста рынка акций на длительном промежутке времени превышает уровень инфляции. Для того чтобы наши инвестиции «поспевали за рынком», нам надо наращивать VA-цель быстрее, чем растет инфляция.
Сравнительные данные для следующей модификации двух методов приведены в третьей строчке таблицы на рис. 5.3. В этом случае ежемесячные инвестиции по методу DCA увеличивались на 0,64 %, а VA-цель каждый месяц увеличивалась на $1 + 0,79 %. Согласно Эдлесону, параметры 0,64 % и 0,79 % экспериментально подбираются таким образом, чтобы в период с 1926 по 1991 г. использование двух методов привело к формированию портфелей примерно одинакового размера. Ежемесячное увеличение на 0,79 % соответствует среднегодовому уровню роста примерно в 9,9 %. Как мы уже знаем, это число соответствует среднегодовому уровню роста рынка акций США в период с 1926 по 1991 г. При таких параметрах метод VA уверенно «обыгрывает» метод DCA примерно на 1 %. Таким образом, ежемесячное увеличение на 0,79 % позволяет поддерживать адекватный уровень инвестиций по методу VA. Таким образом, метод VA «поспевает» за рынком.
Майкл Эдлесон произвел дополнительные исследования вышеописанных методов на основе рыночных данных в период с 1990 по 2005 г. [1]. Напомним, что этот период сопровождался бурным ростом рынка, бумом интернет-компаний, их крахом и последующим восстановлением рынка к 2005 г. Сравнительные данные для периода 1926–2005 гг. и отдельно – для периода 1990–2005 гг. приведены, соответственно, в строчках 4 и 5 таблицы на рис. 5.3. Как видно из этих данных, метод VA обеспечивает лучшие показатели, чем метод DCA и в этих рыночных условиях.
Математик Пол Маршалл проверил гипотезу о преимуществе метода VA по сравнению с методом DCA и опубликовал результаты в своей статье в 2000 г. [5]. Маршалл использовал статистические методы для большего диапазона рыночных данных. Он пришел к выводу, что метод VA действительно позволяет получить более высокую производительность инвестиций, чем метод DCA. Причем достигается это без увеличения уровня риска. Преимущество метода VA над методом DCA увеличивается с ростом инвестиционного периода и волатильности используемых активов.
Использование математических принципов, заложенных в методах VA и DCA, позволяет реализовать еще одну функцию, очень полезную для инвестора: расчет примерных регулярных инвестиций, необходимых для достижения определенной финансовой цели на фиксированном отрезке времени. Вывод математических уравнений, применяемых для этого, выходит за рамки этой книги. Этот подход очень подробно описан в книге Майкла Эдлесона [1]. Мы же ограничимся описанием двух готовых формул и примерами их использования.
Итак, введем еще одно понятие: VA-путь. VA-путь показывает, каким должен быть уровень средств на нашем счету в каждом инвестиционном периоде для достижения конечной инвестиционной цели. Формула, приведенная ниже, построена исходя из инвестиционного периода в один месяц. Она учитывает следующие составляющие: рост от ожидаемого возврата инвестиций на наш портфель, от наших месячных инвестиций и от роста этих месячных инвестиций.
V(t) = C × t × (1 + R)^t. (5.1)
В этой формуле символ ^t означает операцию возведения в степень t. Значение R рассчитывается по следующей формуле:
V(t) обозначает значение VA-пути на каждом инвестиционном периоде t; С – первоначальный уровень инвестиций; g – уровень роста, на который инвестор готов увеличивать регулярные инвестиции; r – ожидаемый ежемесячный уровень возврата на инвестиции от используемого актива или портфеля. Формула 5.1 помогает рассчитать необходимый уровень инвестиций для каждого инвестиционного периода с учетом результатов уровня дохода на существующий портфель в предшествующие периоды. В зависимости от реального поведения рынка на каждом периоде инвестору необходимо инвестировать большие или меньшие суммы в последующем периоде. Однако, если рынок демонстрирует поведение, близкое к прогнозируемому, инвестору нужно будет осуществлять ежемесячные инвестиции в ожидаемых рамках.
Допустим, инвестор планирует получить сумму в размере $100 000 после 20 лет инвестиций. Он готов увеличивать средние ежемесячные инвестиции на 0,5 % в месяц и ожидает получить уровень среднего совокупного дохода на свой инвестиционный портфель в размере 1 % в месяц. Для нашего случая R = = (0,005+0,01)/2 = 0,0075. Для 20 лет t = 12 × 20 = 240 месяцев (инвестиционных периодов). Подставляем переменные в уравнение по формуле 5.1:
$100 000 = C × 240 × (1,0075)^240
или
Подставляя полученное значение C в формулу 5.1, получаем удобную формулу 5.2 для расчета VA-цели для каждого месяца t в период между 1-м и 240-м месяцем:
V(t) =69,34 × t × (1,0075)^t. (5.2)
Пример того, как выглядит VA-путь для некоторых месяцев представлен в таблице на рис. 5.4.
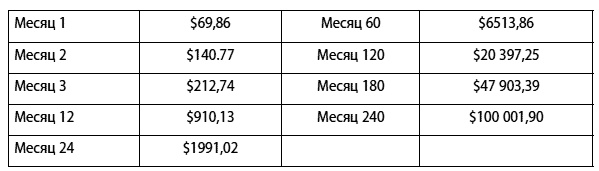
Рис. 5.4. Пример VA-пути для некоторых месяцев
Для полноценной реализации VA-метода инвестор должен стремиться достичь эти ежемесячные VA-цели путем приобретения, а иногда и продажи активов. Придерживаясь VA-пути, инвестор приближается к своей финансовой цели. Этот путь схож с ключевыми ориентирами на карте: сверяя с ними свое реальное местоположение, путешественник все увереннее приближается к цели. На рис. 5.5 VA-путь для нашего примера представлен в графическом виде.



