Результаты построения множественной регрессии, приведенные в таблице 4.4.1, демонстрируют, что коэффициенты, выражающие влияние исторической волатильности, количества дней до экспирации и количества базовых активов, оказались статистически значимыми на очень высоком уровне достоверности. Вероятность того, что отличие расчетных значений этих коэффициентов от нуля было получено случайно, крайне низка (менее 0,1 %). Традиционные методы интерпретации множественной регрессии позволяют составить следующую формулу для прогноза изменчивости прибыли:
Стандартное отклонение = 893,11 + 14,67 × Волатильность – 376,4 × Log (Кол-во базовых активов) + 8,29 × Кол-во дней до экспирации
Следует относиться с большой осторожностью к интерпретации и использованию этой формулы. В частности, из таблицы 4.4.1 следует, что параметр intercept (значение, принимаемое зависимой переменной при условии, что значения всех независимых переменных равны нулю) является статистически значимым на высоком уровне достоверности (то есть его отличие от нуля неслучайно). Это означает, что стандартное отклонение прибыли портфелей при условии, что значения всех трех независимых переменных равны нулю, составляет 893,11 (величина intercept). Однако в исследуемом случае такая трактовка абсурдна, поскольку ни одна из трех переменных не может принимать нулевое значение. Следовательно, в данном случае экстраполяция абсолютно недопустима. Поэтому приведенный в таблице 4.4.1 анализ может использоваться не для прогноза степени вариабельности прибыли портфеля в зависимости от выбранного способа распределения капитала, а только для выявления статистической достоверности влияния каждого из анализируемых факторов.
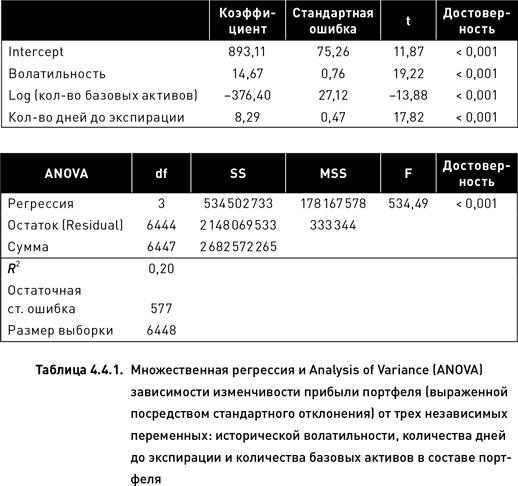
Результаты ANOVA, представленные в таблице 4.4.1, подтверждают, что общая модель множественной регрессии также статистически достоверна на высоком уровне достоверности. Вместе с тем необходимо отметить, что значение коэффициента детерминации достаточно невелико (R² = 0,2). Это означает, что все три исследованных фактора объясняют лишь 20 % дисперсии зависимой переменной. Логично предположить, что оставшиеся 80 % дисперсии объясняются, помимо неизбежной случайной ошибки, многими факторами, составляющими суть торговой стратегии. Поэтому относительно небольшое значение коэффициента детерминации вполне объяснимо и не является удивительным.
4.4.2. Мера концентрации капитала в портфеле
В этом разделе мы сравним между собой различные показатели с точки зрения равномерности распределения капитала внутри портфеля. Предположим, что в соответствии с торговой стратегией имеется сумма M, выделенная на первом этапе реализации системы управления капиталом. Допустим, что существует n комбинаций – кандидатов на включение в портфель. В каждую из этих комбинаций может быть инвестирована доля w от капитала M. Теоретически могут существовать два предельных случая при распределении капитала. Вся сумма M может быть инвестирована в единственную комбинацию; при этом все прочие комбинации получают нулевую часть капитала (то есть вовсе не включаются в портфель). Другой предельный случай – это равномерное распределение средств, когда каждая комбинация получает одинаковую долю капитала равную M/n.
На практике оба эти сценария встречаются крайне редко. Обычно капитал распределяется неким промежуточным образом, когда потенциально более привлекательные комбинации получают больше капитала, чем менее привлекательные. Привлекательность определяется с помощью специальных показателей, семь из которых были подробно рассмотрены в разделах 4.3.1 и 4.3.2. Портфели, в которых большая часть капитала распределена между несколькими комбинациями, мы будем называть «концентрированными». А портфели, в которых доля капитала, инвестированного в разные комбинации приблизительно одинакова, будем называть «равномерными».
Степень концентрированности капитала является важным показателем для сравнения между собой различных способов распределения капитала. Дело в том, что уровень диверсификации портфеля чрезвычайно важен для управления и контроля рисков. Ранее мы оценивали диверсификацию портфеля по количеству базовых активов, включенных в его состав (рис. 4.4.5). Однако, даже если портфель состоит из комбинаций, относящихся к большому количеству базовых активов, он может тем не менее быть слабо диверсифицированным, если большая часть капитала сконцентрирована в комбинациях, относящихся к одному (или нескольким) активам. Если же капитал распределен более-менее равномерно между комбинациями, относящимися к разным базовым активам, то такой портфель является более диверсифицированным и, соответственно, менее рискованным.
Ранее мы выражали степень концентрированности капитала путем расчета коэффициента вариации весов различных комбинаций, входящих в состав портфеля (раздел 4.3.2, таблица 4.3.2). Поскольку сейчас мы обрабатываем большой массив данных (6448 портфелей для каждого из семи показателей распределения капитала) целесообразно будет ввести другой, более удобный и статистически более обоснованный показатель. Назовем его «индекс концентрированности портфеля».
Продемонстрируем расчет индекса концентрированности на примере данных таблицы 4.3.2 и двух показателей, математического ожидания прибыли и дельты. На основе каждого из этих двух показателей был сформирован портфель, состоящий из 20 комбинаций. Данные портфели отличаются друг от друга только набором весов w, в соответствии с которыми распределяется капитал между комбинациями. Для каждого портфеля отсортируем все комбинации по весу инвестированного в них капитала. Рассчитаем кумулятивную пропорцию капитала для двух комбинаций с наибольшим весом, затем для трех комбинаций и так далее до 20-й комбинации. Построим функцию зависимости кумулятивной пропорции от пропорции комбинаций в портфеле (отношение числа комбинаций, для которых было рассчитано данное значение кумулятивной функции к общему количеству комбинаций в портфеле). Например, для портфеля, сформированного по показателю «математическое ожидание прибыли», три комбинации с наибольшими весами имеют суммарный вес 0,34 (значение функции кумулятивной пропорции). Соответствующее этому весу значение пропорции комбинаций в портфеле равно 3/20 = 0,15. Это означает, что 34 % капитала сосредоточено в 15 % комбинаций.
На рис. 4.4.6 показаны две функции кумулятивной пропорции, соответствующие показателям «математическое ожидание прибыли» и «дельта» (данные взяты из таблицы 4.3.2). Используя эти функции, можно рассчитать, в каком проценте комбинаций (от общего числа комбинаций в портфеле) сосредоточено 50 % капитала. Это и будет значением индекса концентрированности портфеля. Для показателя «математическое ожидание прибыли» индекс равен 0,25, а для дельты он равен приблизительно 0,42. Это означает, что при распределении капитала по матожиданию прибыли 50 % капитала оказалось вложенным в 25 % комбинаций, а при формировании портфеля по показателю дельты половина капитала была вложена в 42 % комбинаций. Следовательно, в данном примере использование показателя «математическое ожидание прибыли» приводит к более концентрированному распределению капитала и, соответственно, созданию менее диверсифицированного портфеля.

