4.4. Одномерная система распределения капитала
4.4.1. Факторы, влияющие на распределение капитала по различным показателям
В этом разделе мы будем исследовать влияние различных факторов на распределение капитала с помощью различных показателей. Если в предыдущих разделах мы просто продемонстрировали технику формирования портфеля в заданный момент времени из ограниченного и заранее определенного количества комбинаций, то теперь мы рассмотрим функционирование полноценной торговой стратегии на длительном временном интервале.
Процесс формирования портфеля будем моделировать по исторической базе цен акций и их опционов за период 2002–2010 гг. В качестве базовых активов для построения опционных комбинаций будем использовать акции из списка S&P 500. Будем использовать дневные цены закрытия на акции и соответствующие им последние котировки спроса и предложения опционов (в качестве текущей цены опциона принимается середина спреда).
Обозначим через S = {s1, s2…, sm} множество всех рассматриваемых акций. Двигаясь по истории из прошлого в будущее, будем каждый день T строить для каждой акции si из S множество опционных комбинаций по следующим правилам. Определим три ближайшие даты экспирации опционов. Для каждой даты экспирации, отстоящей от T на определенное количество торговых дней в будущее, возьмем множество всех опционов пут и колл на акцию si, имеющих страйки, удаленные от текущей цены акции не более чем на 10 %. Материалом для формирования портфеля будет множество коротких комбинаций типа стрэддл и стрэнгл, построенных с соблюдением следующих условий. При построении стрэнглов допускаются только те варианты, для которых страйк пута меньше страйка колла. Стрэддлы и стрэнглы состоят из равного числа опционов пут и колл.
В результате для каждого дня прошлого и каждой из трех ближайших экспираций получается широкий набор опционных комбинаций. Для каждой из них подсчитаем значение математического ожидания прибыли по логнормальному распределению. Выберем те комбинации, у которых значение этого критерия больше 1 % от объема инвестиций. Будем строить портфель из элементов этого множества путем распределения $100 000 (объем средств, выделенных на первом этапе процесса управления капиталом). Капитал будем распределять по одному из семи показателей, описанных в предыдущих разделах:
1) эквивалент позиции в акциях;
2) обратно пропорционально премии;
3) математическое ожидание прибыли на основе логнормального распределения;
4) вероятность получения прибыли на основе логнормального распределения;
5) дельта;
6) асимметрия;
7) VaR.
На дату экспирации будем фиксировать прибыль или убыток каждого портфеля.
Сравнительный анализ этих показателей будет фокусироваться на следующем вопросе: насколько портфели, сформированные с помощью различных показателей, отличаются друг от друга с точки зрения их доходности. Другими словами, в какой степени доходность портфеля зависит от показателя, с помощью которого распределялся капитал между элементами портфеля.
В предыдущем разделе для того, чтобы выразить степень различия портфелей с точки зрения их внутренней структуры, мы использовали коэффициент вариации весов отдельных элементов портфеля. Поскольку вес портфеля всегда положителен, c применением коэффициента вариации не возникает проблем. Однако в этом разделе мы будем сравнивать различные методы распределения капитала на основе реализовавшейся прибыли портфеля, которая может быть отрицательной (убыток). Поскольку в данном случае коэффициент вариации – вычисляемый как отношение стандартного отклонения (всегда положительно) к среднему (положительно или отрицательно) – может оказаться отрицательной величиной, его применение для оценки изменчивости (степени различия портфелей) невозможно. Поэтому нам придется выражать изменчивость с помощью стандартного отклонения, не нормированного на величину среднего.
Чем чреват такой отказ от нормировки? Из практики известно, что во многих случаях стандартное отклонение имеет положительную корреляцию со средним. В таких случаях тренды, наблюдаемые в динамике изменчивости (или другие зависимости), могут по существу быть трендами среднего, а не изменчивости. Нормировка же позволяет устранить этот недостаток. Поэтому, прежде чем приступить к нашим исследованиям (в которых мы вынуждены отказаться от нормировки), необходимо установить, существует ли в нашем случае взаимозависимость между средним и стандартным отклонением. Использование ненормированного стандартного отклонения будет допустимо только в том случае, если такой зависимости не существует.
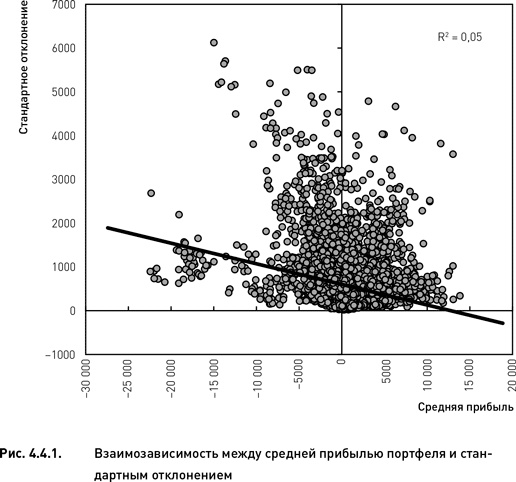
Для того чтобы установить, существует ли прямая зависимость между средним и стандартным отклонением, мы рассчитали их значения на каждую дату создания портфелей. Среднее и стандартное отклонение вычислялись по величине прибыли семи портфелей, сформированных по семи разным показателям. На основе полученных данных мы провели регрессионный анализ, результаты которого представлены на рис. 4.4.1. Как следует из рисунка, прямая зависимость между средним и стандартным отклонением в данном случае не наблюдается. Более того, существует слабо выраженная обратная зависимость. Несмотря на то что обратная зависимость статистически значима (t = 18,4, p < 0,001), ее влиянием можно пренебречь в силу того, что коэффициент детерминации имеет очень низкое значение (R2 = 0,05). Таким образом, в нашем исследовании допустимо использовать в качестве меры изменчивости стандартное отклонение, не нормированное на величину среднего.
На протяжении всего периода исследования уровень изменчивости прибыли варьировал в довольно широком диапазоне (рис. 4.4.2). В определенные периоды изменчивость была очень высокой. Это означает, что в такие периоды способ распределения капитала имел большое влияние на прибыль портфеля. В то же время в другие периоды наблюдалась низкая изменчивость, что свидетельствует о том, что выбор определенного показателя для распределения капитала внутри портфеля не оказывал заметного влияния на доходность портфеля.
Таким образом, мы установили, что при определенных обстоятельствах выбор способа распределения капитала может оказывать заметное влияние на результаты работы торговой системы, а при других условиях может быть совершенно не важным. Поэтому необходимо установить, от чего зависит степень влияния, оказываемого выбором способа распределения капитала. Иначе говоря, какие факторы делают решение о выборе того или иного показателя, используемого для формирования портфеля, значимым и важным. Для того чтобы ответить на этот вопрос, мы исследуем влияние трех факторов (исторической волатильности, времени создания портфеля и количества разных базовых активов в составе портфеля) на изменчивость прибыли портфелей, отличающихся друг от друга способом распределения капитала.
Историческая волатильность
Для того чтобы установить, влияет ли уровень волатильности рынка на изменчивость прибыли портфелей, сформированных по разным показателям, мы рассчитали величину исторической волатильности индекса S&P 500 для каждой даты создания портфеля (расчет делался на 120-дневном историческом горизонте). Все данные по изменчивости прибыли были сгруппированы и усреднены по уровням исторической волатильности индекса S&P 500. При группировке в качестве дискрета (шага) использовался 1 % волатильности. Например, в одну группу вошли и были усреднены все стандартные отклонения, соответствующие тем датам создания портфеля, когда историческая волатильность находилась в диапазоне от 22 до 23 %. Соответственно, стандартные отклонения, относящиеся к тем датам, когда историческая волатильность находилась в диапазоне от 23 до 24 % вошли в следующую группу. И так далее.

