Для каждого опциона Oi, входящего в состав портфеля, мы имеем опционную дельту:
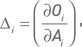
где величины δO1 и δA1 обозначают малые изменения цен опциона и его базового актива соответственно. Это выражение дает наглядное представление о дельте как о скорости изменения цены опциона по отношению к изменению цены его базового актива.
Вычисление дельты Di одного опциона не представляет сложности и реализовано во многих компьютерных программах. Переходя к портфелю, состоящему из опционов на разные базовые активы, мы не можем суммировать дельты разных опционов, поскольку они являются частными производными функций (премий) по разным независимым переменным (ценам акций). Как было сказано выше, эту задачу мы будем решать, вычисляя скорость изменения стоимости опциона по отношению к индексу, а не к отдельным базовым активам. Определим дельту по отношению к индексу как производную цены опциона по значению индекса:
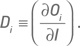
Эту индексную дельту можно также представить в следующем виде:
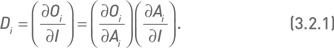
Величина
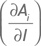 так же, как и бета показывает изменение цены базового актива при изменении индекса (разница между ними в том, что первая является размерной величиной, а вторая – безразмерной, выраженной отношением относительных изменений двух величин). Бета традиционно используется для оценки взаимосвязи между движениями индекса и отдельного актива. Для наших целей будет удобно представить бету в виде следующего отношения:
так же, как и бета показывает изменение цены базового актива при изменении индекса (разница между ними в том, что первая является размерной величиной, а вторая – безразмерной, выраженной отношением относительных изменений двух величин). Бета традиционно используется для оценки взаимосвязи между движениями индекса и отдельного актива. Для наших целей будет удобно представить бету в виде следующего отношения:
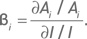
Произведя несложные преобразования
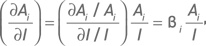
подставим полученное выражение в формулу (3.2.1). Получаем индексную дельту одного опциона:

где Δi – дельта опциона относительно его базового актива. Количество единиц опциона Oi, входящее в состав портфеля, обозначим через xi. Для вычисления индексной дельты Dportfolio всего портфеля суммируем дельты отдельных опционов, входящих в портфель с учетом их количества:
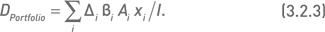
Индексную дельту, рассчитанную по формуле (3.2.3), можно интерпретировать как изменение стоимости портфеля при изменении значения индекса на один пункт. Более удобно выражать изменение стоимости портфеля при изменении индекса на некую процентную величину. Это позволит оценить чувствительность портфеля к относительным изменениям индекса. Например, простое преобразование формулы (3.2.3) позволяет вычислять «процентную индексную дельту» для изменения индекса на 1 %:
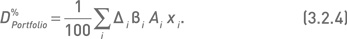
Пример расчета индексной дельты
В качестве примера рассчитаем величину индексной дельты небольшого портфеля, состоящего из опционов на американские акции. Вычисления будем производить относительно индекса S&P 500, хотя для этих целей может использоваться любой другой индекс. В таблице 3.2.1 представлен портфель, состоящий из семи коротких стрэддлов, взятых в разных количествах (приблизительно обратно пропорциональных ценам соответствующих акций). Портфель был создан 2 января 2009 г. из опционов с ближайшей датой экспирации (16 января 2009 г.). Текущее значение индекса на 2 января 2009 г. составляло 931,8. Коэффициенты бета акций рассчитаны по ценам дневного закрытия на горизонте истории, равном 120 торговым дням. Дельты опционов вычислены по формулам Блэка – Шоулса с безрисковой ставкой, равной 3,3 %.
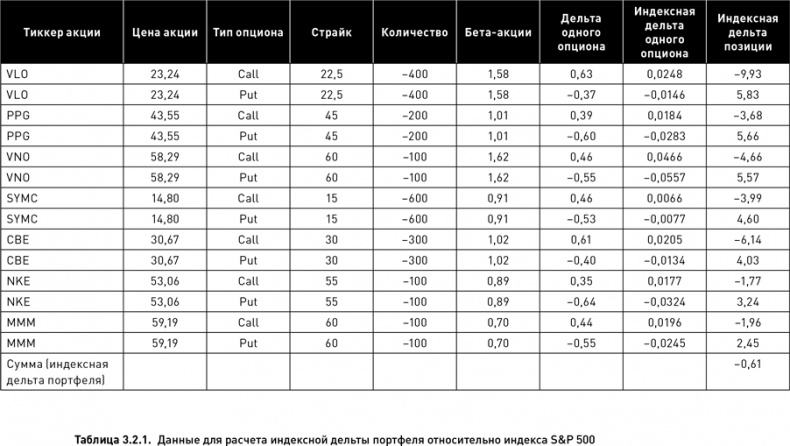
В предпоследней колонке таблицы 3.2.1 приведены индексные дельты одного опциона, рассчитанные по формуле (3.2.2). Например, для колл на акцию VLO получаем Di = (23,24 × 1,58 × 0,63)/931,8 = 0,0248. Произведение индексной дельты одного опциона на его количество в портфеле дает индексную дельту позиции по данному контракту (последняя колонка таблицы). Так, индексная дельта позиции по контракту VLO 22,5 колл равна Di = −400 × 0,0248 = −9,93. Суммирование индексных дельт всех позиций (то есть всех значений, приведенных в последней колонке таблицы) дает индексную дельту портфеля, соответствующую формуле (3.2.3). В данном примере DPortfolio = −0,61. Используя формулу (3.2.4), это значение легко преобразуется в процентную индексную дельту:
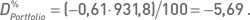
Анализ эффективности использования индексной дельты для оценки риска
Для исследования эффективности индексной дельты нами проведены статистические исследования на исторической базе данных, содержащей восьмилетнюю историю цен опционов и их базовых активов. В качестве базовых активов были задействованы акции, составляющие индекс S&P 500.
На историческом горизонте с начала 2001 г. по начало 2009 г. для каждой даты экспирации была сформирована серия портфелей. Момент создания каждого портфеля отстоял от даты экспирации на разное количество торговых дней. Так, самый «дальний» из портфелей был удален от даты истечения на 60 дней, следующий за ним – на 59 дней и так далее вплоть до последнего портфеля, отстоящего от момента экспирации всего на два дня. Таким образом, на каждую дату экспирации было создано 59 портфелей, отличающихся друг от друга продолжительностью времени, остающегося до дня истечения опционов. Всего было создано от 30 (для 60 дней) до 90 (для двух дней) портфелей для каждого «количества дней до экспирации».

