В этом разделе мы проанализируем три аспекта эффективности случайного поиска:
1. Зависимость эффективности поиска от количества случайно выбираемых узлов. Эффективность будет тестироваться для 100, 200, …, 1000 попыток (всего 10 вариантов количества выбираемых узлов).
2. Влияние формы оптимизационного пространства на эффективность случайного поиска. Как и в предыдущем разделе, мы применим метод случайного поиска к оптимизационным пространствам, соответствующим целевым функциям «прибыль» и «процент прибыльных сделок».
3. Сравнение эффективности случайного поиска с двумя методами целенаправленного поиска – покоординатным спуском и методом Хука−Дживса (которые оказались наиболее эффективными среди других методов целенаправленного поиска).
Для анализа эффективности случайного поиска воспользуемся теми же показателями, которые использовались для сравнения четырех методов целенаправленного поиска (таблица 2.7.1).
Как и следовало ожидать, значения всех показателей растут по мере увеличения количества случайно выбранных узлов (рис. 2.7.5 и 2.7.6). Однако темпы этого роста зависят от каждого конкретного показателя. Более того, форма зависимости эффективности поиска от количества попыток различна для разных показателей. Процент оптимальных решений, совпадающих с глобальным максимумом, увеличивается линейно с ростом количества проверенных узлов. С другой стороны, процент оптимальных решений, расположенных в оптимальной области, и среднее значение целевой функции всех оптимальных решений растут нелинейно по мере увеличения количества попыток: в начале рост происходит быстрыми темпами, затем дальнейшее увеличение числа попыток приводит лишь к незначительному росту эффективности поиска.
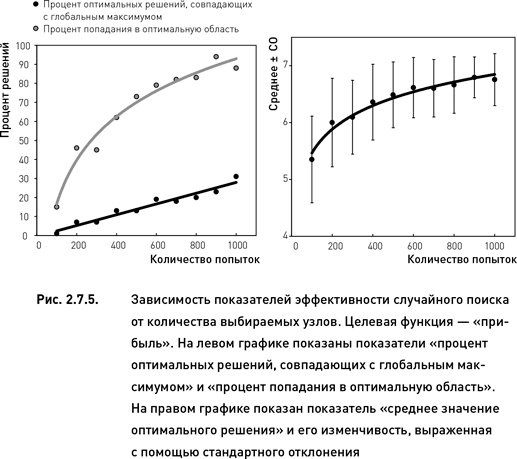
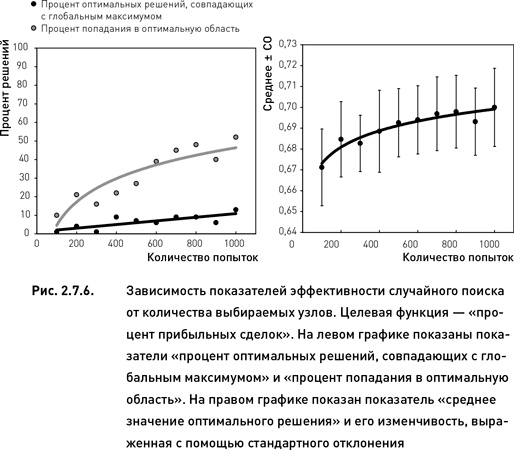
Эффективность случайного поиска выше для оптимизационного пространства, соответствующего целевой функции «прибыль» по сравнению с пространством «процент прибыльных сделок» (сравни левые графики рис. 2.7.5 и 2.7.6). Это полностью совпадает с результатами целенаправленного поиска, полученными в предыдущем разделе. Кроме того, для целевой функции «прибыль» изменчивость показателя «среднее значение оптимального решения» уменьшается при увеличении числа попыток (правый график рис. 2.7.5). В то же время для целевой функции «процент прибыльных торговых циклов» такая зависимость не наблюдается (правый график рис. 2.7.6).
По показателю «процент оптимальных решений, совпадающих с глобальным максимумом» случайный поиск уступает покоординатному подъему и методу Хука−Дживса. Однако при использовании достаточного количества попыток случайный поиск оказывается более эффективным по двум другим показателям. Для целевой функции «прибыль» случайный поиск становится эффективнее покоординатного подъема по показателям «среднее значение оптимального решения» и «процент попадания в оптимальную область» начиная с 400 попыток. При использовании 500 попыток данный метод превосходит и вторую методику, Хука−Дживса (сравни рис. 2.7.5 с данными таблицы 2.7.1). Для целевой функции «процент прибыльных сделок» случайный поиск становится эффективнее покоординатного подъема и метода Хука−Дживса по проценту попаданий в оптимальную область начиная с 600 попыток. По среднему значению оптимального решения случайный поиск превосходит эти две методики начиная с 700 попыток (сравни рис. 2.7.6 с данными таблицы 1).
Проведенный анализ приводит к ряду полезных выводов относительно применимости случайного поиска для оптимизации торговых стратегий. В общем виде можно утверждать, что при увеличении числа попыток до определенного уровня, вероятность того, что наилучшее из полученных решений окажется достаточно близким к глобальному максимуму, может быть удовлетворительно велика. В частности, случайный поиск может использоваться, если (1) размеры оптимизационного пространства позволяют исследовать порядка 20 % его ячеек и (2) имеется предварительная информация об унимодальности оптимизационного пространства. Последнее возможно в тех случаях, когда в процессе построения стратегии уже производилась оптимизация путем полного перебора, в ходе которой форма пространства была установлена. Если пространство оказывается близким по форме к тому, которое было получено нами для целевой функции «прибыль» (рис. 2.2.2), то при дальнейших доработках и модификациях стратегии можно использовать метод случайного поиска.
2.8. Построение оптимизационной инфраструктуры: решения и компромиссы
Построение инфраструктуры для оптимизации торговых стратегий вообще и опционных стратегий в частности требует принятия целого ряда сложных решений, от продуманности которых зависит не только количество ресурсов, затрачиваемых на выполнение необходимых процедур, но и надежность получаемого результата. В большинстве случаев сложность решений заключается в необходимости поиска компромисса между минимизацией времени, необходимого для вычислений, и максимизацией объема получаемой информации, необходимой для эффективного поиска оптимума.
В частности, выбор структуры оптимизационного пространства требует принятия нескольких компромиссных решений. Первое из них – размерность оптимизации, определяемая количеством параметров. Полный набор параметров, требующих оптимизации, определяется логикой стратегии, однако решение о том, какие из них будут оптимизироваться «техническими методами», аналогичными описанным в этой главе, а какие будут зафиксированы исходя из априорных соображений (или с помощью научных методов), безусловно, является продуктом компромисса. Чем меньше параметров необходимо оптимизировать, тем проще процедуры и тем меньше риск оверфитинга. С другой стороны, отказ от оптимизации (фиксация параметров) повышает риск упустить прибыльный вариант стратегии. Следующее решение – это выбор диапазона допустимых значений параметров и шага оптимизации. Здесь необходим компромисс между затрачиваемым временем и получаемой информацией. Поэтому решение зависит в большой степени от объема вычислительных ресурсов, доступных разработчику стратегии.
Сокращение времени вычислений является важным, но далеко не единственным вызовом, стоящим перед разработчиком стратегий. Принципиально важным является решение о составе, количестве и относительной важности целевых функций, используемых в процессе оптимизации. Мы рекомендовали основывать решение этого вопроса на степени взаимозависимости между разными функциями и на объемах содержащейся в них дополнительной информации. После того как набор целевых функций определен, необходимо выбрать метод многокритериального анализа, что также является нетривиальной задачей. Многие другие факторы, в том числе робастность и устойчивость оптимизационного пространства, могут оказывать решающее влияние на результаты оптимизации. Выбор метода целенаправленного поиска также является одним из основных компромиссов (разрешаемых на основе предварительного изучения свойств оптимизационного пространства), от которого зависит надежность конечного оптимального решения.

