Чтобы получить статистически достоверные результаты, для каждой из двух целевых функций и для каждого метода было проведено по 300 полных оптимизационных циклов. Все циклы отличались друг от друга только стартовой точкой, с которой начинался поиск оптимального решения. Сравнительный анализ эффективности разных методов оптимизации базируется на следующих пяти показателях (в каждом случае они рассчитываются на основе 300 данных):
1. Процент оптимальных решений, совпадающих с глобальным максимумом (когда оптимизационный алгоритм остановился на узле с наибольшим значением целевой функции).
2. Процент оптимальных решений, расположенных в оптимальной области. Значения целевой функции этих решений не должны быть ниже определенного порогового значения.
3. Процент неудовлетворительных оптимальных решений. Целевые функции этих решений имеют значения, не превышающие определенную пороговую величину.
4. Среднее значение целевой функции всех оптимальных решений, рассчитанное на основе 300 полных оптимизационных циклов.
5. Среднее количество вычислений, необходимых для выполнения полного оптимизационного цикла.
В таблице 2.7.1 показаны значения всех пяти показателей эффективности для четырех методов целенаправленного поиска. Когда в качестве целевой функции использовалась прибыль, метод Хука−Дживса оказался наиболее эффективным. В 69 % случаев в качестве оптимального решения был выбран узел, соответствующий глобальному максимуму (соответственно, в 31 % случаев алгоритм поиска остановился, не найдя узел с самым высоким значением целевой функции). По проценту попаданий в оптимальную область (72 % от всех случаев) и по среднему значению целевой функции, рассчитанному для всех решений (6.43), данный метод также значительно превзошел все другие методы. Единственный показатель, по которому метод Хука−Дживса оказался несколько хуже (совсем ненамного) метода покоординатного подъема – это процент неудовлетворительных оптимальных решений (15 %). Однако существенным недостатком этого метода оказалась его затратность по времени. Для завершения одного полного оптимизационного цикла пришлось произвести в среднем 1279 вычислений. Это значительно больше, чем количество вычислений, требуемых для других методов.
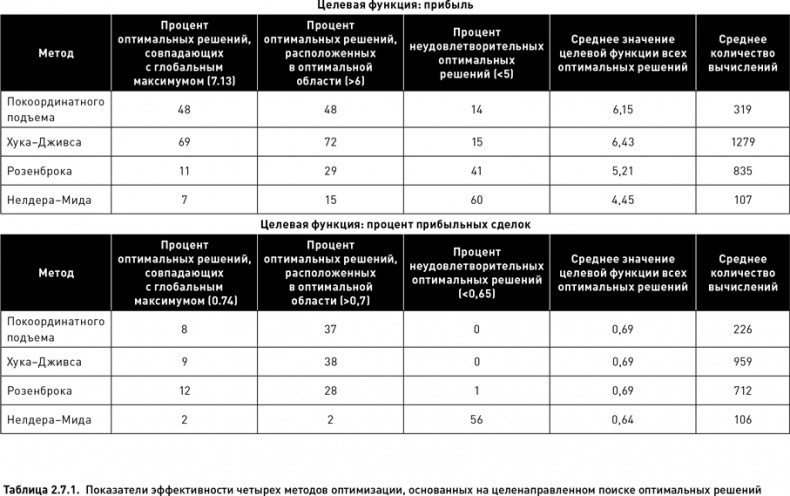
На втором месте по эффективности оптимизации унимодальной целевой функции (прибыль) находится метод покоординатного подъема. Хотя он несколько уступает по всем показателям (кроме процента неудовлетворительных оптимальных решений) методу Хука−Дживса, его несомненным достоинством является относительно небольшое количество требуемых вычислений (в среднем 319, что в четыре раза меньше, чем требуется при использовании метода Хука−Дживса).
Метод Розенброка существенно уступает по эффективности двум предыдущим методикам. Лишь в 11 % случаев с помощью этого метода удалось обнаружить узел глобального максимума, а в 41 % случаев алгоритм остановился на ячейках, относящихся к областям с низкими значениями целевой функции. Кроме того, количество вычислений, требуемых для нахождения оптимальных решений, по методу Розенброка оказалось достаточно большим (в среднем 835), находясь на втором месте после метода Хука−Дживса.
Наихудшие результаты были получены для метода Нелдера – Мида. Хотя количество вычислений для этого метода оказалось наименьшим по сравнению с другими методами, все показатели его эффективности находятся на очень низком уровне. Всего в 7 % случаев решение совпало с глобальным максимумом и лишь в 15 % случаев оптимальное решение находилось в оптимальной области. В 60 % случаев решения оказались неудовлетворительными.
Для другого оптимизационного пространства, построенного на основе целевой функции «процент прибыльных сделок», эффективность методов покоординатного подъема Хука−Дживса и Розенброка оказалась приблизительно одинаковой (если не считать того, что последний метод был несколько хуже по показателю «процент попаданий в оптимальную область»). Метод Нелдера – Мида вновь показал наихудшие результаты. Такая низкая эффективность данного метода весьма удивительна. Возможно, она объясняется тем, что для успешного применения этого метода необходимо тщательно подбирать стартовые условия (размер симплекса), а также значения его многочисленных параметров (коэффициенты отражения, сжатия, редукции, расширения). Мы же выбрали размер симплекса произвольно, а для коэффициентов приняли обычно используемые значения. Вероятно, для получения удовлетворительных результатов необходима более тонкая настройка параметров и некоторые априорные предположения о свойствах оптимизационного пространства.
Для оптимизационного пространства, соответствующего целевой функции «процент прибыльных сделок», эффективность всех четырех методов оптимизации оказалась значительно ниже по сравнению с их эффективностью на пространстве функции «прибыль». Это подтверждает наше предположение о том, что форма оптимизационного пространства оказывает значительное влияние на эффективность оптимизации. По всей видимости, унимодальные пространства с относительно широкой оптимальной зоной легче поддаются оптимизации методами целенаправленного поиска, чем полимодальные пространства с большим количеством раздробленных оптимальных областей.
2.7.3. Случайный поиск
До сих пор мы рассматривали два подхода к оптимизации – полный перебор, требующий вычисления целевой функции во всех узлах оптимизационного пространства, и целенаправленный поиск. Возможен еще один подход, состоящий в вычислении целевой функции в случайно выбранных узлах оптимизационного пространства. Безусловно, случайный поиск представляет собой самый простой способ оптимизации. Для его реализации достаточно выбрать случайным образом заданное количество узлов и рассчитать значения целевой функции для каждого из них. После этого узел с наибольшим значением выбирается в качестве оптимального решения. Этот метод настолько примитивен, что зачастую вообще не рассматривается в качестве приемлемой методики. Тем не менее во многих случаях (и по многим показателям) случайный поиск может дать достаточно эффективные результаты, не уступающие методам целенаправленного поиска.
Основной и единственный фактор, влияющий на эффективность случайного поиска, – это количество выбираемых ячеек. Чем больше делается попыток, тем выше вероятность того, что оптимальное решение совпадет с глобальным максимумом или будет лежать в непосредственной близости от него. При этом количество попыток должно определяться в зависимости от размеров оптимизационного пространства. В наших примерах это пространство состоит из 3600 ячеек. Если для случайного поиска в таком пространстве использовать 100 попыток, то обследованными окажутся менее 3 % ячеек, что, очевидно, недостаточно для нахождения удовлетворительного оптимального решения. Однако если оптимизационное пространство состоит из 500 ячеек, то 100 попыток составят 20 %, что может оказаться достаточным.

