6. Производим поиск в новом (перпендикулярном) направлении и находим узел с наибольшим значением целевой функции (пятая точка с координатами 34 и 215).
7. Начиная с этого узла, повторяем цикл исследующего поиска методом покоординатного подъема. Фиксируем значение параметра «число дней до экспирации» на значении 34 и вычисляем целевую функцию для всех значений параметра «период истории для расчета HV». Максимальное значение функции оказалось в узле с координатами 34 и 140 (шестая точка).
8. Фиксируем период истории на значении 140 и вычисляем целевую функцию для всех дней до экспирации. Максимум функции приходится на узел с координатами 30 и 140 (седьмая точка).
9. Повторяем процедуру поиска по образцу. Определяем направление от пятой точки на седьмую точку (левая нижняя стрелка на рис. 2.7.3) и вычисляем значение целевой функции во всех узлах, пересекаемых данным направлением. Оказывается, что ни в одном из узлов указанного направления значение целевой функции не превосходит значение седьмой точки.
10. Строим направление, перпендикулярное направлению, указанному левой стрелкой (не показано на рисунке), и производим поиск вдоль этого направления. Оказывается, что и в этом направлении не находится ни одного узла, превосходящего по величине целевой функции седьмой узел.
11. Повторяем цикл исследующего поиска. Фиксируем значение параметра «число дней до экспирации» на значении 30 и вычисляем целевую функцию для всех значений параметра «период истории для расчета HV». Максимальное значение функции оказывается в узле с координатами 30 и 105 (восьмая точка).
12. Как мы уже видели в предыдущих примерах (метод Хука−Дживса), дальнейшего улучшения не происходит и, следовательно, алгоритм останавливается. Оптимальным решением является узел номер 8.
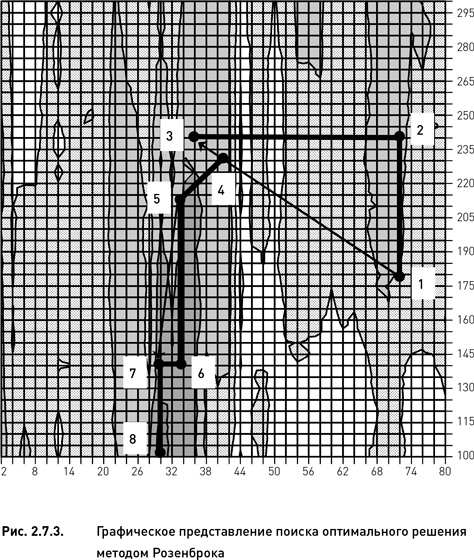
Метод Розенброка представляет собой усовершенствование методов покоординатного подъема и Хука−Дживса. В некоторых случаях он может заметно улучшить эффективность поиска, однако это происходит далеко не всегда. В определенных условиях, зависящих в основном от формы и структуры оптимизационного пространства, эффективность поиска может не только не повыситься, но даже снизиться.
Метод Нелдера – Мида
Существуют две разновидности метода Нелдера – Мида (называемый также методом деформируемого многогранника, симплексным поиском, поиском методом амебы) – первоначальная, с использованием правильного симплекса, и усовершенствованная, с использованием деформируемого симплекса (в этом разделе мы рассмотрим усовершенствованную разновидность). Название отчасти может вводить в заблуждение, поскольку известен симплекс-метод линейного программирования, решающий задачу оптимизации с линейной целевой функцией при линейных ограничениях, с которым описываемый метод не имеет почти ничего общего. Под симплексом понимается многогранник в n-мерном пространстве, имеющий n + 1 вершину. Его можно рассматривать как обобщение треугольника на случай более чем двух измерений. Треугольник, в свою очередь, является примером симплекса в двумерном пространстве.
В процессе оптимизации симплекс, образно говоря, перекатывается в пространстве параметров, приближаясь к экстремуму. Вычислив значения целевой функции в его вершинах, находим худшее из них и перемещаем симплекс так, чтобы прочие вершины остались на месте, а взамен вершины с худшим значением была бы включена вершина, симметричная «худшей» относительно центра тяжести симплекса. Особенно наглядно это можно представить в двумерном случае, когда симплекс, а им в этом случае является треугольник, перекатывается через сторону треугольника, противолежащую к «худшей» вершине. Таким образом симплекс приближается к экстремуму, пока такие движения не перестанут улучшать целевую функцию. Наилучшая из полученных вершин является оптимальным решением. Однако у такого метода есть очевидный недостаток. Когда мы окажемся в непосредственной близости экстремума, так что расстояние от центра симплекса до экстремума станет меньше стороны симплекса, он потеряет способность приближаться к экстремуму. В этом случае можно уменьшить размер симплекса, при том, что он сохранит исходную форму, и продолжить поиск, повторяя это уменьшение размеров при потере способности приближаться к экстремуму, пока длина стороны не станет меньше шага оптимизации.
Метод деформируемого симплекса (деформируемого многогранника), помимо «перекатывания» его в пространстве параметров, включает и изменение его формы (что объясняет еще одно его название – «метод амебы»). Если у метода правильного симплекса нет иных параметров, кроме длины ребра симплекса, то здесь вводится система из четырех выбираемых исследователем параметров: коэффициент отражения α (обычно принимаемый равным 1), коэффициент растяжения σ (часто принимаемый равным 2), коэффициент сжатия γ (часто выбираемый равным 0,5), коэффициент редукции ρ (также может быть выбран 0,5). Как показывает опыт, выбор значений коэффициентов может оказаться критическим для получения удовлетворительных результатов оптимизации. Иногда рекомендуют выбирать коэффициенты γ и σ так, чтобы они не были взаимно обратными, например 2/3 и 2.
Алгоритм метода Нелдера – Мида состоит из следующих шагов:
1. Выбираются n + 1 точка начального симплекса x1, x2 … xn+1. Это могут быть любые точки, не принадлежащие n-мерной гиперплоскости. В двумерном случае, когда симплекс является треугольником, достаточно, чтобы три точки не лежали на одной прямой.
2. Точки упорядочиваются согласно значениям целевой функции (при условии, что ставится задача максимизации функции):
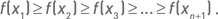
3. Вычисляется точка x0, являющаяся центром тяжести фигуры, вершины которой совпадают с точками симплекса, за исключением «худшей» точки xn + 1:
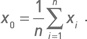
Для двумерной оптимизации x0 располагается посредине отрезка, соединяющего лучшую и среднюю (по значениям целевой функции) точки треугольника.
4. Шаг отражения. Вычисляем отраженную точку:
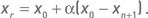
Если значение целевой функции в отраженной точке лучше, чем во второй «худшей» точке xn, но при этом не лучше, чем в наилучшей x1, то отраженная точка заменяет в симплексе удаленную из него «худшую», и алгоритм возвращается на шаг 2 (симплекс «перекатился», уйдя от «худшей» точки в сторону увеличения целевой функции). Если значение целевой функции в «отраженной точке» лучше, чем во всех исходных точках, переходим к шагу 5.

