Существует достаточно простой, хоть и затратный с точки зрения времени, способ решения этой проблемы. Если из содержательных соображений невозможно обосновать наличие в оптимизационном пространстве единственного экстремума, являющегося глобальным максимумом, следует многократно повторить процедуру «поиск экстремума при разных стартовых условиях» (то есть каждый раз начинать оптимизацию с разных узлов пространства). Стартовые узлы можно распределить равномерно в оптимизационном пространстве или выбрать случайным образом. Хотя достижение экстремума в этом случае не гарантируется, с практической точки зрения вероятность его получения может быть доведена до приемлемого уровня. Разумеется, чем больше попыток будет сделано, тем выше вероятность того, что хотя бы одна из них приведет к нахождению глобального максимума (однако и временные затраты также быстро возрастают). Чем больше оптимизационное пространство, тем больше попыток придется сделать.
Второй недостаток заключается в том, что найденное в результате целенаправленного поиска решение не несет в себе информацию о значениях целевой функции в узлах, соседствующих с узлом оптимального решения. Это означает, что мы не имеем возможности определить свойства оптимальной области, окружающей найденный экстремум. Следовательно, мы не в состоянии оценить степень робастности оптимального решения. Как обсуждалось в разделе 2.5, робастность является одним из основных показателей надежности оптимизации. Решить эту проблему можно только одним способом – вычислить значения целевой функции во всех узлах, окружающих найденные экстремумы. После этого можно оценить их робастность (используя одну из методик, описанных в разделе 2.5) и выбрать наилучший вариант в качестве оптимального решения.
2.7.1. Обзор основных методов целенаправленного поиска
Метод покоординатного подъема
Метод покоординатного подъема (обычно в названии этого метода используется слово «спуск», однако, как уже объяснялось ранее, для оптимизации торговых стратегий предпочтительно решать задачу максимизации прибыли) состоит в том, что последовательно производится поиск по каждому параметру, выбирая их один за другим по очереди. Алгоритм данного метода можно представить в следующем виде.
1. Выбирается стартовый узел, с которого начинается процесс оптимизации (выбор начальной точки требуется для инициации любого метода целенаправленного поиска). Выбор может быть случайным, осознанным (то есть основанным на предварительных знаниях разработчика) либо вычисленным (например, если будет производиться множество повторяющихся оптимизаций, то стартовые узлы могут распределяться в оптимизационном пространстве равномерно).
2. Поскольку параметры оптимизируются не одновременно, а последовательно, необходимо определить их очередность. В большинстве случаев очередность не имеет большого значения. Однако если какой-либо параметр более важен, чем другие, то начинать оптимизацию нужно именно с него.
3. Начиная со стартовой точки, находится наилучшее решение по первому параметру. Поиск его осуществляется каким-либо методом одномерной оптимизации. В большинстве случаев допустимо использовать полный перебор, поскольку количество вычисляемых узлов в этом случае относительно невелико. При исследовании первого параметра значения всех других параметров остаются зафиксированными на значениях стартового узла.
4. Переход к оптимизации по следующему параметру производится после того, как найдено наилучшее решение по первому. Вновь производится одномерная оптимизация, при этом значения всех других параметров остаются зафиксированными на значениях узла, найденного в ходе оптимизации первого параметра.
5. Закончив один оптимизационный цикл (заключающийся в одномерной оптимизации каждого из параметров), возобновляем процедуру, начиная с первого по списку параметра. Процесс останавливается после того, как очередной оптимизационный цикл не находит решение, превосходящее по значению целевой функции предыдущее.
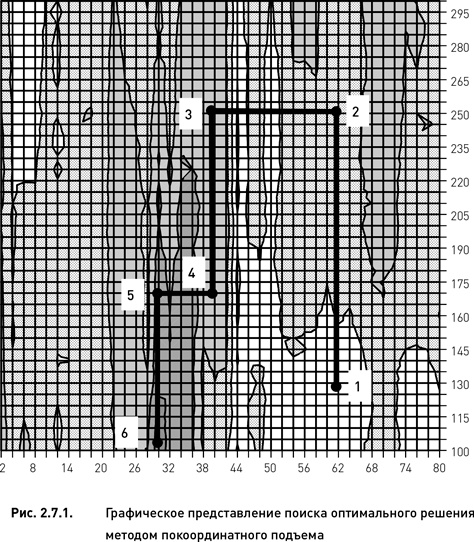
Рассмотрим практическое применение данного алгоритма на примере оптимизации базовой дельта-нейтральной стратегии по целевой функции «прибыль» (оптимизационное пространство показано на рис. 2.2.2). Для того чтобы представить процедуру поиска оптимального решения визуально, ограничим области допустимых значений параметров диапазонами 2–80 для параметра «число дней до экспирации» и 100–300 для параметра «период истории для расчета HV». Выполнение алгоритма происходит следующим образом:
1. Выбираем стартовую точку. Предположим, что случайным образом был выбран узел с координатами 60 и 130. На рис. 2.7.1 данный узел отмечен номером 1.
2. Зафиксировав параметр «число дней до экспирации» на значении 60, вычисляем целевую функцию для всех значений параметра «период истории для расчета HV» (одномерная оптимизация методом полного перебора).
3. Определяем узел с максимальным значением целевой функции. В данном примере таким узлом является узел с координатами 30 и 250 (точка номер 2 на рис. 2.7.1).
4. Фиксируем значение параметра «период истории для расчета HV» на значении 250 и вычисляем целевую функцию для всех значений параметра «число дней до экспирации». Максимальное значение функции оказалось в узле с координатами 40 и 250 (третья точка).
5. Фиксируем число дней до экспирации на значении 40 и вычисляем целевую функцию для всех значений периода истории. Попадаем на следующий узел с координатами 40 и 170 (четвертая точка).
6. Фиксируем период истории на значении 170 и вычисляем целевую функцию для всех дней до экспирации. Попадаем на пятую точку с координатами 30 и 170.
7. Фиксируем число дней до экспирации на 30 и вычисляем целевую функцию для всех значений периода истории. Попадаем на шестую точку с координатами 30 и 105.
8. Фиксируем период истории на значении 105 и вычисляем целевую функцию для всех дней до экспирации. Выясняем, что максимум целевой функции приходится на исходный узел (точка номер 6). Это означает, что дальнейшего улучшения не происходит и, следовательно, алгоритм останавливается. Оптимальным решением является последний узел (номер 6).
Простой по своей логике и легко реализуемый, метод покоординатного подъема, однако, не очень эффективен. Представим себе ситуацию, когда двумерная оптимизационная поверхность имеет оптимальную область в форме узкого «горного хребта», протянувшегося с «северо-запада» на «юго-восток». Если высота хребта повышается в «юго-восточном» направлении, то, применив этот алгоритм, мы выйдем на гребень хребта и не сможем найти улучшения, поскольку для этого надо будет менять два параметра одновременно. Это сильно ограничивает применимость данного метода.
Метод Хука−Дживса
Этот метод был разработан с целью уменьшить вероятность возникновения ситуаций, в которых метод покоординатного подъема останавливается преждевременно, не найдя удовлетворительного оптимального решения. Он включает в себя последовательное применение двух процедур – исследующего поиска и поиска по образцу, повторяемых до нахождения неулучшаемого оптимума. По сравнению с методом покоординатного подъема применение метода Хука−Дживса существенно сокращает вероятность остановки алгоритма, не достигнув экстремума. Алгоритм метода Хука−Дживса имеет следующий вид.

