Применяя данную методику, необходимо учитывать, что k и h выражены в разных единицах измерения. Первая величина выражена в количестве узлов, а вторая – это значение целевой функции, которое может быть любым (проценты, доллары, любой другой показатель). Поэтому S является безразмерной величиной, которая, хотя и пропорциональна реальной площади оптимальной поверхности (и может использоваться для сравнения между собой разных оптимальных областей), не является площадью в истинном смысле. Во избежание недоразумений в дальнейшем мы будем называть этот показатель «условной площадью». Необходимо, чтобы k и h имели приблизительно одинаковую размерность (например, если максимум целевой функции h = 5, а k = 70, то следует преобразовать k путем нормирования его значения на 10. Кроме того, величина h не должна быть меньше 1, поскольку в противном случае возведение в квадрат (см. формулу 2.5.1) не увеличит, а уменьшит результирующую величину.
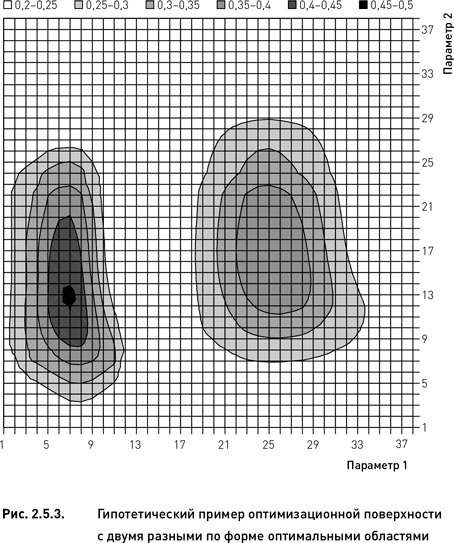
Продемонстрируем практическое применение этой методики. В гипотетическом примере, представленном на рис. 2.5.3, левая область состоит из 185 узлов; значение целевой функции узла с максимальной высотной отметкой равно 0,47 (то есть k = 185, h = 0,47). Для правой области k = 266, h = 0,40. Для того чтобы привести переменные k и h к единой размерности, следует разделить k на 100 и умножить h на 10 (чтобы соблюсти условие h > 1). Воспользовавшись формулой 2.5.1, получим:

Показатель условной площади левой оптимальной области меньше показателя правой области. Это означает, что, несмотря на то что левая область имеет большую высоту, правая является предпочтительной. Следовательно, в данном случае преимущество более широкой и покатой поверхности правой области (то есть преимущество по признаку робастности) перевесили преимущество более высокого значения целевой функции левой области.
Теперь рассмотрим пример, основанный на реальных рыночных данных. На правом графике рис. 2.5.2 имеются три области с высотными отметками выше 10 (напомним, что данная оптимизационная поверхность является продуктом трансформации исходной поверхности, полученной путем свертки трех функций полезности). Обозначим их как «левая», «средняя» и «правая». Все три области имеют близкие по величине площади основания (kleft = 10, kmiddle = 13, kright = 14) и высотные отметки (hleft = 14,09, hmiddle = 13,45, hright = 11,91), что делает выбор одной из них затруднительным. Применение нашей методики позволяет сделать объективный выбор. Поскольку k и h имеют одинаковый порядок величин и h > 1, никаких трансформаций не требуется. Подставляя значения в формулу 2.5.1, получим: Sleft = 79,6, Smiddle = 86,9, Sright = 80,2. Следовательно, выбор средней области является в данном случае предпочтительным. Это решение не тривиально, поскольку данная область не имеет ни наибольшую из трех вариантов площадь основания, ни наибольшую отметку. Интересно, что данный пример демонстрирует комбинированное применение двух методик: вначале оптимизационное пространство было трансформировано путем вычисления отношения среднего к стандартному отклонению, а затем выбор оптимальной области осуществлялся по методу оценки геометрии поверхности.
2.6. Устойчивость оптимизационного пространства
В предыдущем разделе мы использовали свойство робастности для выбора оптимального решения в пределах нескольких областей оптимизационного пространства. Говоря о понятии робастности, мы определили его как чувствительность целевой функции определенных узлов оптимизационного пространства к небольшим изменениям оптимизируемых параметров. Поскольку желательным свойством оптимального решения является большая робастность (то есть нечувствительность), то можно сказать, что, выбирая оптимальное решение, мы стремимся найти наиболее устойчивую оптимальную область. Подчеркнем, что в данном контексте речь идет об устойчивости по отношению к оптимизируемым параметрам.
В этом разделе будет рассмотрен другой аспект устойчивости – степень чувствительности оптимизационного пространства к неоптимизируемым параметрам. В процессе параметрической оптимизации, основанной на алгоритмическом вычислении целевой функции, исследуется множество комбинаций оптимизируемых параметров. При этом многие другие параметры остаются неизменным (будем называть такие параметры «фиксированными»). Их значения могут быть подобраны на более раннем этапе (используя научный подход) либо могут задаваться самой идеей и структурой стратегии, заложенной на начальном этапе ее формализации. Устойчивость оптимизационного пространства к небольшим изменениям фиксированных параметров и к незначительным изменениям в структуре стратегии является важным показателем надежности и качества оптимизации.
Поясним эту идею на простом примере. В процессе оптимизации базовой дельта-нейтральной стратегии нами была получена определенная оптимизационная поверхность (рис. 2.2.2). В этом случае оптимизировались только два параметра, значения всех остальных были зафиксированы. В частности, параметр «порог критерия» был зафиксирован на значении 1 % (позиции открывались только для тех опционных комбинаций, для которых ожидаемая прибыль была >1 %). Предположим, что мы увеличили значение данного параметра до 2 %. Далее предположим, что это привело к тому, что форма оптимизационной поверхности изменилась и стала выглядеть иначе (например, так, как показано на левом графике рис. 2.5.2). Если бы столь незначительное изменение фиксированного параметра привело к такому кардинальному изменению поверхности, то мы должны были бы заключить, что эта поверхность неустойчива, а сама оптимизация крайне ненадежна и, следовательно, полагаться на ее результаты весьма рискованно.
2.6.1. Устойчивость по отношению к фиксированным параметрам
Рассмотрим устойчивость оптимизационного пространства базовой дельта-нейтральной стратегии по отношению к фиксированному параметру «порог критерия». На рис. 2.2.2 показана поверхность, полученная для целевой функции «прибыль» при условии, что порог критерия равен 1 %. Увеличим значение этого фиксированного параметра до 3 % и проверим, насколько такое изменение повлияет на форму оптимизационной поверхности.
Напомним, что до изменения фиксированного параметра глобальный максимум имел координаты 30 по параметру «число дней до экспирации» (горизонтальная ось графика) и 105 по параметру «период истории для расчета HV» (вертикальная ось). После увеличения значения фиксированного параметра глобальный максимум сместился и расположен в узле с координатами 16 и 120 соответственно. Учитывая общую площадь оптимизационного пространства, такое смещение глобального максимума нельзя назвать очень существенным (хотя оно безусловно не является пренебрежимо малым).

