Можно сделать вывод, что, принимая решение о включении той или иной целевой функции в систему многокритериальной оптимизации, следует руководствоваться степенью взаимозависимости рассматриваемых функций. Предпочтение нужно отдавать тем из них, которые коррелируют в наименьшей степени. Это обеспечит внесение в систему максимального количества новой, недублирующейся информации. Определяя степень допустимой взаимозависимости (порог коэффициента корреляции, выше которого целевая функция не принимается), необходимо убедиться в том, что корреляция целевых функций не зависит от значений параметров. В случае если такая зависимость существует (как было показано выше), то для принятия решения нужно использовать такой коэффициент корреляции, который был рассчитан на данных, в наибольшей степени соответствующих логике разрабатываемой торговой стратегии.
2.4. Многокритериальная оптимизация
В предыдущем разделе мы рассмотрели вопрос выбора целевых функций для их дальнейшего использования в системе многокритериальной оптимизации. Данный раздел посвящен поиску оптимальных решений с помощью методов многокритериального анализа. Применительно к параметрической оптимизации задача многокритериального анализа состоит в одновременном использовании многих целевых функций (каждая из которых представляет собой отдельный критерий) для упорядочения узлов оптимизационного пространства (каждый из которых представляет собой определенную уникальную комбинацию параметров) по степени их предпочтительности.
Основная проблема многокритериальной оптимизации состоит в том, что полное упорядочение альтернатив может оказаться невозможным по причине их нетранзитивности. Поясним это на простом примере. Будем считать лучшим тот вариант, который превосходит остальные по большинству критериев. Предположим, что при сравнении трех узлов (А, В и С) по значениям трех целевых функций (критериев) был получен следующий результат: A = (1; 2; 3), B = (2; 3; 1), C = (3; 1; 2) – в скобках указаны значения критериев. Очевидно, что по первому и второму критерию узел B предпочтителен узлу A, а C лучше B по первому и третьему критерию. При соблюдении свойства транзитивности из этого должно следовать, что узел C предпочтителен A. Однако это не так, поскольку A превосходит C по двум критериям, второму и третьему.
Проблема нетранзитивности не имеет универсального решения. Тем не менее существуют два основных подхода, позволяющих получить приемлемое оптимальное решение (или несколько решений), несмотря на несоблюдение свойства транзитивности. Первый подход основывается на приведении всех целевых функций к единому критерию, называемому «свертка», второй подход состоит в применении метода Парето.
2.4.1. Свертка
Отказ от одновременного использования нескольких критериев путем замены их новым единственным критерием (представляющим собой некую функцию, аргументами которой являются исходные критерии) составляет суть свертки. Преимуществом свертки является простота реализации и возможность регулировать степень влияния различных критериев на результат оптимизации. Это достигается путем умножения значений критериев на выбранные весовые коэффициенты – чем больше вес данного критерия, тем большее влияние он окажет на окончательный результат многокритериальной оптимизации. Основным недостатком свертки является неизбежная потеря информации при переходе от многомерного вектора критериев к единственному показателю.
Наиболее распространенными являются два вида свертки: аддитивная (сумма или среднее арифметическое значений всех критериев) и мультипликативная (произведение или среднее геометрическое значений всех критериев). Применение мультипликативной свертки возможно, только если критерии неотрицательны (поскольку произведение двух отрицательных значений дают положительную величину), либо если только один из критериев может принимать отрицательные значения. Также нужно учитывать, что если один из критериев равен нулю, то и мультипликативная свертка равна нулю (для аддитивной свертки этого не происходит). В мультипликативной свертке по сравнению с аддитивной большее влияние оказывают критерии, имеющие более низкие значения. Аддитивная свертка наиболее приемлема для критериев, представляющих собой однородные по смыслу и близкие по масштабу значений величины.
Кроме аддитивной и мультипликативной, существует также селективная свертка, когда для каждого узла принимается в качестве значения свертки наименьшее (наиболее консервативный вариант свертки) или наибольшее (наиболее агрессивный вариант) значение из всего набора целевых функций. В книге «Опционы: системный подход к инвестициям» мы предложили методику минимаксной свертки, когда в качестве значения свертки используется произведение наибольшего и наименьшего значений критериев.
При расчете свертки необходимо помнить о том, что критерии могут измеряться в разных единицах и иметь различный масштаб величин. Для приведения их к единой шкале с одинаковыми диапазонами значений можно воспользоваться следующей трансформацией:
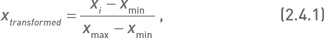
где xi – значение критерия для i-го узла x, xmin и xmax – минимальное и максимальное значение критерия соответственно. Применение этой формулы позволяет привести значение критерия к интервалу от 0 до 1.
Продемонстрируем применение свертки на примере базовой дельта-нейтральной стратегии. В качестве критериев выберем три из четырех целевых функций, показанных на рис. 2.3.1 – прибыль, максимальную просадку и процент прибыльных сделок (коэффициент Шарпа не будет использоваться в силу его сильной скоррелированности с прибылью). Применив формулу 2.4.1, мы привели значения всех трех целевых функций к интервалу от 0 до 1. Построив три варианта свертки (аддитивную, мультипликативную и минимаксную), мы убедились в том, что в данном случае все они дают весьма близкие результаты.
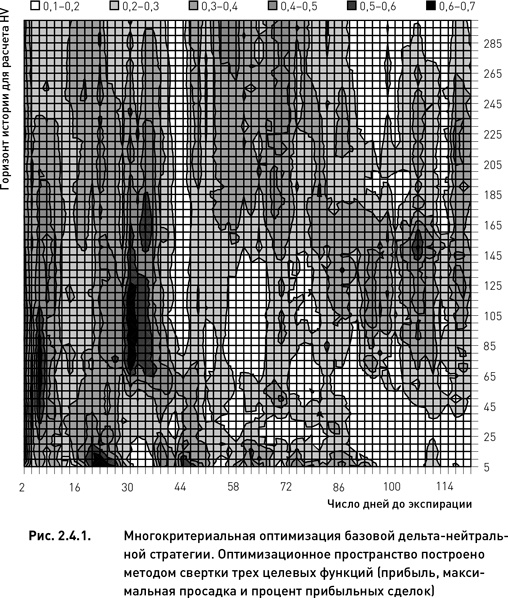
На рис. 2.4.1 показана оптимизационная поверхность минимаксной свертки. Данная поверхность полимодальна и имеет четыре оптимальные области. Три из них имеют относительно обширную площадь, а одна очень мала (поскольку площадь поверхности является одним из важных факторов при выборе оптимального решения, четвертую область можно не рассматривать). Как видим, многокритериальный анализ методом свертки не позволил в данном случае получить единственное оптимальное решение, так как каждая из зон содержит свое оптимальное решение. Следовательно, само по себе построение свертки не решило до конца задачу оптимизации. Необходимо выбрать из трех зон одну. Поскольку все они обладают приблизительно одинаковыми высотными отметками (значение свертки), то выбор должен осуществляться по другому принципу. В следующем разделе мы рассмотрим вопрос выбора оптимальной области на основании характеристик рельефа и количественных оценок робастности потенциальных оптимальных решений.

