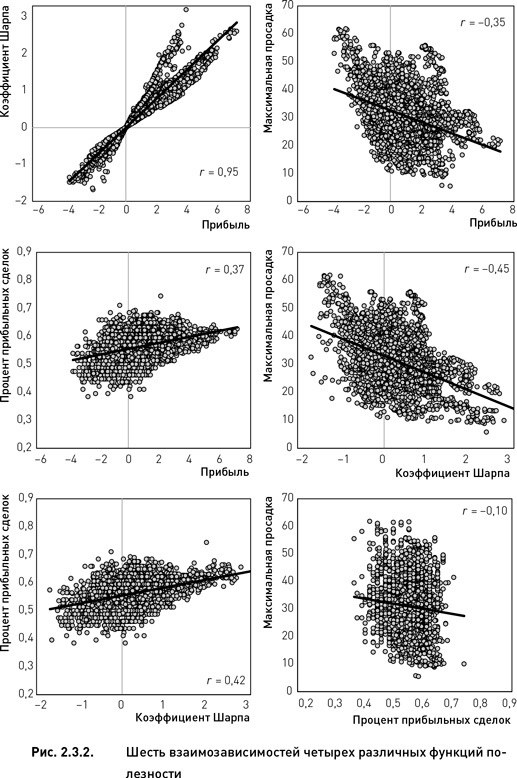
Для того чтобы принять такое решение, необходимо изучить взаимозависимость между этими двумя функциями полезности. Как следует из правого нижнего графика рис. 2.3.2 и низкого коэффициента корреляции (0,10), значения процента прибыльных сделок и максимальной просадки практически не зависят друг от друга. Информация, содержащаяся в этих двух функциях, почти не повторяется (доля не дублируемой информации составляет 99 %). Следовательно, добавление обеих целевых функций в систему многокритериального анализа вполне оправдано.
Таким образом, из четырех рассмотренных нами целевых функций имеет смысл использовать для многокритериальной оптимизации только три (прибыль, процент прибыльных сделок и максимальную просадку). Исключение из многокритериального анализа коэффициента Шарпа оправдывается не только тем, что эта функция почти полностью дублирует функцию прибыли, но еще и тем, что коэффициент Шарпа коррелирует с процентом прибыльных сделок и с максимальной просадкой в гораздо большей степени, чем функция прибыли (средний правый и левый нижний графики рис. 2.3.2).
Описанная выше процедура выбора целевых функций выглядит достаточно просто. Однако необходимо признать, что мы сознательно упростили эту процедуру, для того чтобы излишне не усложнять описание. Теперь мы устраним это упрощение, чтобы продемонстрировать всю сложность и многоплановость процесса выбора подходящих целевых функций.
Дело в том, что взаимозависимости, представленные на рис. 2.3.2, были построены на основании всего набора данных, составляющих оптимизационные пространства целевых функций. Это значит, что данные взаимозависимости строились для полных диапазонов значений двух параметров (2–120 дней для количества дней до экспирации опционов, 5–300 дней для периода истории для расчета HV). Например, для оценки корреляции между прибылью и коэффициентом Шарпа каждому узлу на левом верхнем графике рис. 2.3.1 ставилась в соответствие точка на правом верхнем графике. Полученная в результате такого сопоставления зависимость (верхний левый график рис. 2.3.2) состоит из 3600 точек.
Вместе с тем вполне можно предположить, что степень, и даже направленность, взаимозависимостей между разными целевыми функциями может меняться в зависимости от конкретных значений параметров и, соответственно, от диапазонов их значений. Для того чтобы проверить это предположение, следует рассчитать корреляции для каждого из значений двух параметров по отдельности (то есть нужно проверить, меняются ли корреляции в зависимости от значений параметров).
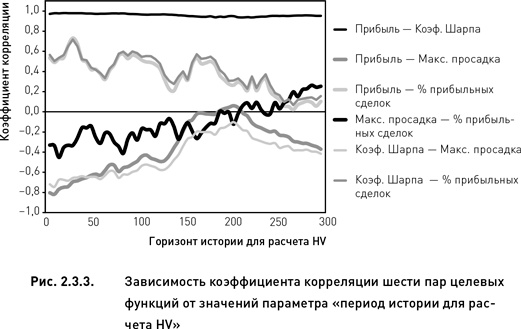
Начнем с параметра «период истории для расчета HV». Корреляции между некоторыми парами целевых функций зависят, а между некоторыми – не зависят от значений этого параметра (рис. 2.3.3). Например, корреляция функций, для которых была отмечена наибольшая степень взаимозависимости (прибыль и коэффициент Шарпа), не меняется на всем диапазоне значений параметра. Все прочие пары функций демонстрируют явно выраженные тренды.
Взаимозависимость пары целевых функций «прибыль» и «процент прибыльных сделок» достаточно высока при низких значениях параметра «период истории для расчета HV». По мере увеличения значений параметра степень скоррелированности двух этих функций снижается и падает до нуля, когда параметр достигает верхней границы диапазона своих допустимых значений. Такой же точно тренд характеризует и взаимозависимость другой пары целевых функций «коэффициент Шарпа» и «процент прибыльных сделок». Такая схожесть трендов не удивительна, принимая во внимание почти абсолютную скоррелированность значений прибыли и коэффициента Шарпа.
Две другие пары целевых функций (прибыль и максимальная просадка, коэффициент Шарпа и максимальная просадка) также демонстрируют почти одинаковый тренд (причина схожести трендов та же, что и в предыдущем случае). Корреляции для этих двух пар при низких значениях параметра достаточно сильны (напомним, что в случае максимальной просадки отрицательный коэффициент корреляции имеет тот же смысл, что и положительная корреляция). По мере увеличения параметра до средних значений корреляция приближается к нулю, а затем вновь уходит в отрицательную область. Когда мы рассматривали те же данные консолидированно (правый верхний и правый средний графики рис. 2.3.2), то могли обнаружить только обратную зависимость для этих пар целевых функций. Детализированный анализ, представленный на рис. 2.3.3, позволяет установить, что в диапазоне средних значений параметра «период истории для расчета HV» корреляции внутри этих двух пар целевых функций отсутствуют вовсе (и, следовательно, содержащаяся в них информация не дублируется).
Взаимозависимость последней пары целевых функций (максимальная просадка и процент прибыльных сделок) демонстрирует повышательный тренд. При низких значениях параметра коэффициент корреляции отрицателен, а, когда параметр достигает своих максимальных значений, корреляция становится положительной (коэффициент корреляции равен нулю, когда «период истории для расчета HV» составляет порядка 200 дней). Вновь заметим, что, когда те же данные рассматривались консолидировано (правый нижний график рис. 2.3.2), то мы не смогли обнаружить какую-либо взаимозависимость между этими целевыми функциями. Из этого можно было сделать не совсем верный вывод о полном отсутствии дублирования информации. Между тем детализированный анализ (рис. 2.3.3) позволяет уточнить, что информация не дублируется только во второй трети диапазона допустимых значений параметра.
Теперь перейдем к рассмотрению влияния второго параметра, «число дней до экспирации опционов» на взаимозависимость целевых функций (рис. 2.3.4). Данный параметр влияет на скоррелированность целевых функций в гораздо большей степени, чем «период истории для расчета HV» (сравни рис. 2.3.3 и 2.3.4). Даже небольшие изменения параметра приводят к весьма существенным изменениям корреляций. Коэффициенты корреляции почти всех пар целевых функций колеблются в очень широком диапазоне (от –0,9 до 0,9). Однако в отличии от предыдущего случая (когда рассматривалось влияние параметра «период истории для расчета HV») влияние количества дней, остающихся до истечения опционов, весьма хаотично. В динамике коэффициентов корреляции отсутствуют всякие признаки трендов.
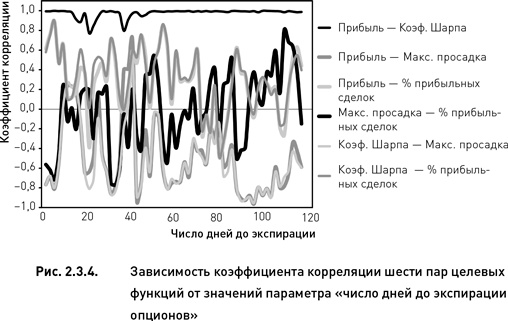
Единственное исключение составляет пара целевых функций «прибыль» и «коэффициент Шарпа». В этом случае коэффициент корреляции не зависит от количества дней до экспирации и сохраняет максимально высокое значение почти на всем диапазоне допустимых значений параметра (рис. 2.3.4). Точно такая же картина наблюдалась для этой пары целевых функций при изучении влияния параметра «период истории для расчета HV» (рис. 2.3.3).





