Кроме того, диапазон допустимых значений не должен обязательно начинаться с наименьших возможных значений параметра, как это было сделано в предыдущих примерах (рис. 2.2.2 и 2.2.3, левый график). Допустим, что разработчик создает стратегию, работающую с более долгосрочными опционами. В этом случае он может задать нижнюю границу на диапазон допустимых значений параметра «число дней до экспирации». Допустим – это будет 60 дней (пусть верхняя граница остается без изменений). Изменение в диапазоне этого параметра потребует внесения изменений и в диапазон второго параметра, поскольку при торговле долгосрочными опционами неразумно оценивать их с помощью критерия, рассчитываемого на основании волатильности, оцененной на более коротком периоде, чем период обращения самих опционов. Следовательно, диапазон значений параметра «период истории для расчета HV» должен быть также ограничен снизу 60 днями (для того чтобы количество значений каждого параметра в пределах допустимого диапазона было одинаковым, верхнюю границу ограничим значением 210).
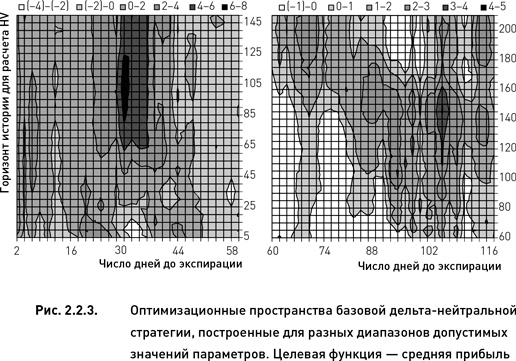
Рассмотрим оптимизационную поверхность, полученную для новых диапазонов допустимых значений параметров (правый график рис. 2.2.3). Совершенно очевидно, что в этом случае результаты оптимизации будут другими. Глобальный максимум теперь имеет другие координаты – 106 по горизонтальной оси и 145 по вертикальной. В том случае, когда рассматривалось более широкое пространство, этот узел являлся локальным максимумом. Теперь же, когда более высокий экстремум остался за рамками рассмотрения, локальный максимум превратился в глобальный. Значение целевой функции в этом узле составляет 4,1 % (ниже глобального максимума более широкого пространства, 7,1 %).
Таким образом, можно сделать вывод, что диапазон значений параметров влияет на форму оптимизационного пространства и в значительной степени определяет выбор окончательного оптимального решения. В целом, чем больше область допустимых значений параметров, тем больше шанс, что максимум целевой функции попадет в исследуемое оптимизационное пространство. Однако при этом уменьшается шанс найти этот максимум в процессе оптимизации, поскольку, во-первых, возникает необходимость проверять большее количество узлов и, во-вторых, из-за сложности поверхности возрастает риск «застрять» на локальных максимумах.
2.2.3. Шаг оптимизации
Шаг оптимизации не оказывает определяющего влияния на общую форму оптимизационного пространства, однако он влияет самым прямым образом на глубину его проработки. Чем шире шаг, тем больше деталей рельефа оптимизационного пространства может быть упущено в процессе оптимизации. Например, из-за слишком широкого шага оптимизации можно вовсе не обнаружить узкий пик функции полезности. Следовательно, при увеличении шага объем информации о целевой функции уменьшается.
Для рассматривавшейся ранее оптимизационной поверхности (рис. 2.2.2) использовался шаг два дня (для параметра «число дней до экспирации») и пять дней (для параметра «период истории для расчета HV»). Теперь мы увеличим эти значения – до четырех и 10 дней соответственно – и посмотрим какой эффект это окажет на информативность пространства. Левый график рис. 2.2.4 демонстрирует поверхность, полученную в результате увеличения шага. Сравнивая эту поверхность с рис. 2.2.2, мы видим, что, несмотря на уменьшение деталей, область глобального максимума сохранилась. Ранее узел глобального максимума имел координаты 30 по горизонтальной оси и 105 по вертикальной, теперь глобальный максимум имеет координаты 30 и 100. Хотя узел, имевший самое высокое значение целевой функции (7,1 %) исчез, его место в качестве глобального максимума занял соседний узел, целевая функция которого имеет весьма близкое значение (7 %).
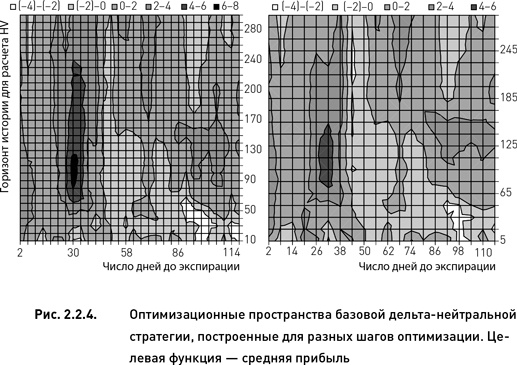
Продолжим процедуру укрупнения шага, увеличив его значения до шести дней для параметра «число дней до экспирации» и 15 дней для параметра «период истории для расчета HV». Количество деталей рельефа уменьшилось еще больше (правый график рис. 2.2.4). Кроме того, полностью исчезла прежняя оптимальная область, располагавшаяся ранее вдоль 30-й вертикали и содержавшая узел глобального максимума. Новый глобальный максимум теперь имеет координаты 32 и 125, а значение новой целевой функция деградирует до 5,5 %. Отсюда следует вывод, что по мере укрупнения шага оптимизации происходит ухудшение находимых оптимальных решений.
Вместе с тем увеличение шага оптимизации имеет и свои плюсы. Несмотря на сдвиг в координатах глобального максимума и ухудшение находимых решений, новая оптимальная область по-прежнему остается приблизительно в том же районе оптимизационного пространства, что и при более детальной проработке. При этом само пространство получается более гладким. Преимущество сглаживания заключается в том, что большинство незначительных локальных экстремумов исчезает из оптимизационного пространства. В результате уменьшается вероятность того, что процесс оптимизации (использующий более экономные способы поиска оптимального решения, чем метод полного перебора) остановится на локальном максимуме.
Следовательно, увеличение шага оптимизации, с одной стороны, уменьшает шанс того, что максимум целевой функции, попадет в исследуемое оптимизационное пространство, но, с другой стороны, снижает количество вычислений и повышает эффективность поиска за счет устранения незначительных локальных экстремумов.
2.3. Целевые функции и их применение для базовой дельта-нейтральной стратегии
С помощью целевой функции мы оцениваем и сравниваем между собой меру полезности различных комбинаций параметров. Поэтому выбор целевой функции является одним из ключевых элементов, во многом определяющим эффективность оптимизации. Каждая функция создает оптимизационное пространство, имеющее свои характерные особенности. Оптимизационные пространства разных функций полезности могут быть достаточно близкими по своей форме, а могут существенно отличаться друг от друга. В этой главе мы рассмотрим различные функции полезности, создающие как похожие, так и весьма далекие по форме пространства.
В большинстве случаев невозможно ограничиться одной функцией полезности. Обычно приходиться использовать не менее трех-четырех функций одновременно. Иногда их количество бывает гораздо большим (до 10 и даже более). Использование большого количества целевых функций особенно актуально для оптимизации опционных торговых стратегий, поскольку в этом случае приходится оценивать не только стандартные параметры доходности и риска, но также особые характеристики, специфичные для опционов. В главе 1 мы рассматривали множество таких функций, когда говорили о характеристиках опционных портфелей. Увеличение количества целевых функций приводит к необходимости разработки специальных методик многокритериального анализа. Значительная часть материала текущей главы будет посвящена этому непростому вопросу.

