В этой главе мы ставим себе целью рассмотреть форму и свойства некоего типичного пространства, взяв в качестве примера базовую дельта-нейтральную стратегию. Два основных параметра этой стратегии (которые широко обсуждались в главе 1) зафиксируем на следующих значениях: порог критерия > 1 %, диапазон страйков 10 %. В предыдущей главе мы уже частично касались темы оптимизации, когда обсуждали эти параметры. Однако в разделе 1.6 мы находили оптимальные значения, полагаясь по большей части на научный подход, а не используя технические приемы оптимизации, которым посвящена эта глава.
Далее мы будем рассматривать оптимизационное пространство, соответствующее двум параметрам базовой дельта-нейтральной стратегии: «количество дней до экспирации опционов» и «горизонт истории для расчета НV». Смысл первого из двух параметров уже частично обсуждался нами в главе 1. Значение этого параметра оказывает самое прямое воздействие на структуру формируемого портфеля. Второй параметр относится к длине исторического периода, используемого для расчета исторической волатильности. В свою очередь, историческая волатильность используется для расчета значений критерия «математическое ожидание прибыли на основе логнормального распределения», на основании которого генерируются сигналы на открытие торговых позиций. Несмотря на то что влияние данного параметра непрямое, он также является одним из самых важных в данной стратегии, поскольку от его значений в большой степени зависит, какие опционные комбинации войдут в состав портфеля.
2.2.1. Размерность оптимизации
Одним из основных факторов, определяющих форму оптимизационного пространства, является набор параметров. При определении этого набора, первый и один из главных вопросов, на которые должен ответить разработчик, – это количество параметров, требующих оптимизации. В принципе, необходимо придерживаться правила минимизации числа параметров. Для этого есть две основные причины. Во-первых, чем больше параметров участвует в оптимизации, тем больше степеней свободы имеет оптимизируемая система и тем больше риск оверфитинга. Во-вторых, большая размерность оптимизации требует чрезмерного количества вычислений, что может быть технически нереализуемо. С другой стороны, чрезмерное сокращение количества оптимизируемых параметров может не позволить найти удовлетворительное решение, в результате чего потенциально прибыльная торговая стратегия может быть отвергнута как бесперспективная. По этим соображениям при построении автоматизированных торговых стратегий обычно используют от двух до четырех параметров.
Одномерная оптимизация
Хотя задача одномерной оптимизации наиболее проста (и редко используется на практике), ее можно рассматривать как частный случай более сложной многомерной оптимизации. С ее помощью легче понять постановку задачи, методы решения и трудности, возникающие при исследовании сложных оптимизационных пространств. Алгоритмы решения многомерных задач часто сводятся к последовательному многократному решению одномерных задач и не могут быть поняты без умения их решать.
На рис. 2.2.1 показаны три примера одномерного оптимизационного пространства. Каждая линия на графике демонстрирует оптимизацию параметра «период истории для расчета HV» базовой стратегии для трех вариантов фиксированного значения второго параметра «число дней до экспирации опционов». Область допустимых значений для оптимизируемого параметра составляет диапазон от пяти до 300 дней, шаг оптимизации – пять дней. Полное оптимизационное пространство в этом случае состоит из 60 узлов. Данная оптимизация проводилась на исторических данных за 10-летний период. В качестве функции полезности используется показатель прибыли (среднее значение за весь период оптимизации). Ни одно из трех оптимизационных пространств, представленных на рис. 2.2.1, не является гладким. Это неудивительно, поскольку данный рисунок построен на реальных рыночных данных, а абсолютно гладкими могут быть только пространства, построенные с помощью аналитически заданных формул. Тем не менее неизбежный статистический «шум» не мешает рассмотреть основные паттерны, характерные для каждой из линий и классифицировать эти оптимизационные пространства в соответствии с их модальностью.
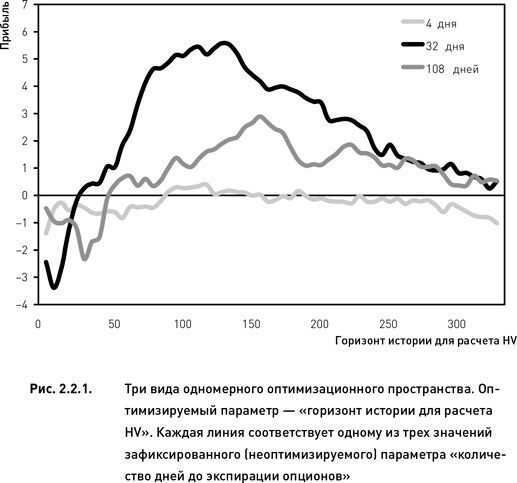
Каждая линия на рис. 2.2.1 иллюстрирует одну из трех основных форм оптимизационного пространства. Когда параметр «число дней до экспирации» был зафиксирован на значении «32 дня», оптимизационное пространство оказалось унимодальным. В этом случае целевая функция имеет единственный глобальный максимум, соответствующий значению «120 дней», оптимизируемого параметра «период истории для расчета HV». Локальные максимумы отсутствуют. Необходимо оговориться, что утверждение об отсутствии локальных максимумов и унимодальности данного оптимизационного пространства является в определенном смысле субъективным мнением. Поскольку данная линия не является гладкой, то в принципе можно утверждать, что локальные максимумы имеются, например, в точках «105 дней» (слева от глобального максимума) и «230 дней». Тем не менее, поскольку в масштабе всего пространства данные пики очень невелики, мы склонны относить их категории «статистического шума». При необходимости процесс определения модальности может быть формализован, что позволит избежать субъективных суждений.
Примером полимодального оптимизационного пространства может служить линия, полученная в том случае, когда параметр «число дней до экспирации» был зафиксирован на значении «108 дней». Глобальный максимум этой оптимизации приходится на значение «145 дней» параметра «период истории для расчета HV». В отличие от предыдущего примера целевая функция этого оптимизационного пространства имеет явно выраженный локальный максимум, приходящийся на «205 дней» параметра «период истории для расчета HV».
И, наконец, третья линия на рис. 2.2.1 является примером безмодального оптимизационного пространства. В том случае, когда сигналы на открытие торговых позиций генерировались только для краткосрочных опционов (параметр «число дней до экспирации» зафиксирован на значении «четыре дня»), целевая функция оказалась приблизительно нулевой почти для всего диапазона параметра «горизонт истории».
Поскольку в примерах, приведенных на рис. 2.2.1, целевая функция была исследована на всем диапазоне допустимых значений параметра (так называемый метод полного перебора), то выбор оптимального решения на первый взгляд кажется очевидным. Для унимодальной функции – это 120 дней, для полимодальной – 145 дней. Однако оптимальное решение не обязательно должно совпадать с глобальным или локальным экстремумом. Существует дополнительный, не менее важный критерий выбора оптимального решения – его робастность. Принимая во внимание понятие робастности, выбор 120 дней в качестве оптимального решения может оказаться не самым лучшим. Увеличение параметра (до 125, 130 и т. д.) ведет к достаточно резкому падению целевой функции. В то же время если в качестве оптимального решения выбрать 195 дней, то все соседние значения параметра (как в сторону увеличения, так и в сторону уменьшения) имеют достаточно высокие значения целевой функции. В данном примере глобальный максимум унимодальной функции полезности является более робастным оптимальным решением (он находится на более широком возвышении), чем глобальный максимум полимодальной функции (который расположен на достаточно узком пике).

