Диапазон вероятностей от 0 до 1,0 кумулятивного распределения разбивается на части – квантили – методом медиан интервального ряда. В таблице именно так разделена ожидаемая стоимость. Например, чтобы разделить диапазон вероятности ожидаемой стоимости на пять частей, нужно взять квантили 0,1; 0,3; 0,5; 0,7 и 0,9. Эти квантили будут представлять собой среднее арифметическое в диапазонах значений 0–0,2; 0,2–0,4; 0,4–0,6; 0,6–0,8 и 0,8–1,0 соответственно.
Квантиль 0,5 равнозначен медиане, поскольку с каждой его стороны находится ровно половина возможных значений. Медиана не обязательно совпадает со средним, то есть центром нормального распределения. Медиана – это просто центр диапазона значений. Среднее – это сумма произведений всех вероятностей на соответствующие значения: именно так мы получили ожидаемую стоимость обнаружения нефти $1 млн.
Чтобы объединить концепцию кумулятивного распределения с деревом решения и принимать существенные управленческие решения, нужно представить себе все вероятные значения прибыли от нефтяной скважины. Диапазон значений можно изобразить в виде веера событий. Кому-то может не хватить терпения для представления бесконечных возможностей в виде ветвей дерева, и тут выручит кумулятивная вероятность.
Рисуем кумулятивное распределение. Чтобы представить кумулятивное распределение в графической форме, как показано ниже, следует опираться на собственное суждение и данные исследований. Нужно задать себе ряд вопросов:
• При каком значении в 50 % случаев результат оказывается выше или ниже заданного значения (медиана)?
• Каким будет значение нижнего конца спектра (квантиль 0,10)?
• Каким будет значение верхнего конца спектра (квантиль 0,90)?
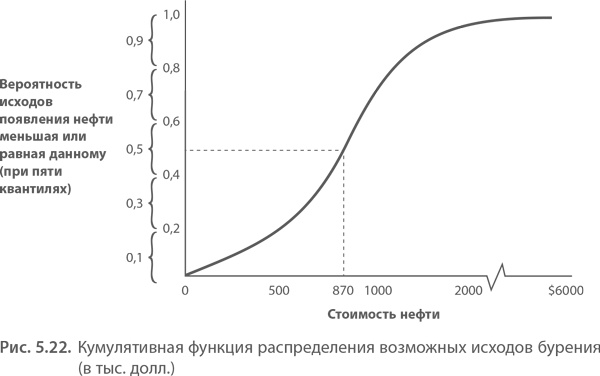

Ответив на эти вопросы, вы сможете представить кумулятивную стоимость возможных исходов. Ограничившись пятью исходами или пятью квантилями кумулятивного распределения, вы можете изобразить веер событий и их вероятностей на дереве решений в виде пяти ветвей.
Ожидаемый денежный эквивалент будет таким же, как при первом рассмотрении, но только потому, что с самого начала для удобства была задана правильная величина ожидаемой стоимости.
Сокращенный вариант такого анализа называют методом Тьюки – Пирсона. Вместо пяти квантилей используется всего три – 0,05; 0,5 и 0,95. Соответствующие этим квантилям вероятности – 0,185; 0,63 и 0,185.
Применительно к крупным задачам дерево решений строится с помощью компьютерных симулякров Монте-Карло, самый популярный из них – Oracle. Дерево и параметры «веера событий» кумулятивного распределения включены в компьютерную модель. Программа прогоняет множество сценариев событий, чтобы дать вам представление, чем может обернуться дело. Некоторые из компаний Fortune 500 используют этот метод.
Кумулятивное распределение и анализ методом квантилей можно применять к ситуациям, в которых ожидаемая стоимость ветви дерева решений неопределенна. Однако важнее всего суждение аналитика. Дерево – это всего лишь инструмент, который МВА обязан использовать в сочетании со своими знаниями и интуицией.
Регрессионный анализ и прогнозирование
Модели линейной регрессии применяются в самых разных деловых ситуациях для установления зависимости между переменными, которые, как подсказывает аналитику его интуиция, должны быть между собой связаны. После того как зависимость установлена, ее можно использовать для прогнозирования. Обычно регрессионный анализ используется для соотнесения продаж с ценой, рекламой и рыночными факторами; курса акций с доходами и процентными ставками; затрат на производство с объемами производства. Но, конечно, анализ можно использовать также и для ответов другие вопросы: «Как влияет температура воздуха на продажу мороженого?» Независимой переменной в этом случае является температура. Это та переменная, от которой, как предполагается, зависит все остальное. Зависимой переменной будет объем продаж. Температура на улице влияет на объем продаж, но не наоборот.
Для регрессионного анализа необходимо собрать данные, чтобы установить отношения между переменными. Когда данных много, как в случае информации по изменениям температуры и объема продаж за год, можно построить график, откладывая по оси X значения температуры, а по оси Y – объемы продаж. Цель регрессионного анализа – составить уравнение прямой, которая «наилучшим образом» отображает зависимость, то есть провести линию между нанесенными на график точками так, чтобы «значение суммы квадратов отклонений точек от линии было наименьшим». При работе методом наименьших квадратов приходится бесконечно складывать, вычитать и умножать. Для облегчения расчетов нужны калькулятор или программа построения электронных таблиц.
Краткое повторение курса алгебры
Перед рассмотрением примера регрессивного анализа вспомним основы алгебры. Как вы помните, прямая описывается следующей формулой:

Программа построения электронных таблиц рассчитывает линейное уравнение (Y = mX + b), описывающее связь между независимой и зависимой переменными. Программа определяет, можно ли использовать прямую, «наилучшим образом» отображающую эту связь, в качестве точного инструмента прогнозирования.
Пример: регрессионный анализ продаж мороженого
Владелец сети из двадцати магазинов по продаже мороженого Ben & Jerry’s заметил, что объемы продаж растут и снижаются вместе с ростом и понижением температуры воздуха. Решив определить точную математическую зависимость между объемом продаж и сезонными температурами, он собрал данные по ежемесячным объемам продаж за предыдущие пять лет, а в Национальной метеорологической службе получил данные по среднемесячным температурам. В результате получилась следующая таблица (5.3):


Используя функцию «Regression» программы построения электронных таблиц, владелец получил следующий результат (табл. 5.4):

