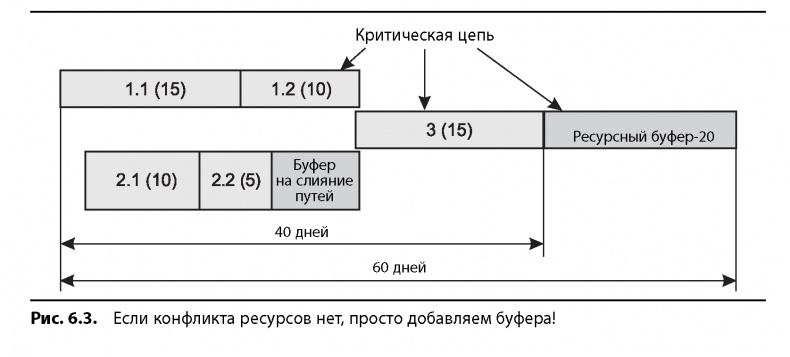
Далее мы добавляем проектный буфер и буферы на слияние путей. Поскольку исполнитель (ресурс) у всех операций один, в данном проекте нет необходимости добавлять ресурсный буфер (рис. 6.3).
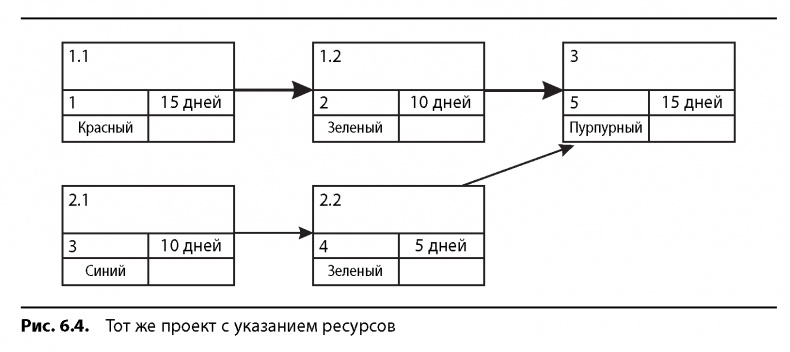
Теперь рассмотрим тот же небольшой проект, но уже с конфликтом ресурсов. Рис. 6.4 показывает последовательность операций в виде диаграммы PERT и без временной шкалы. Необходимые ресурсы в диаграмме обозначены разными цветами. Под этими цветами можно понимать, например, различные профессии (инженер, музыкант, оператор станков и т. п.).
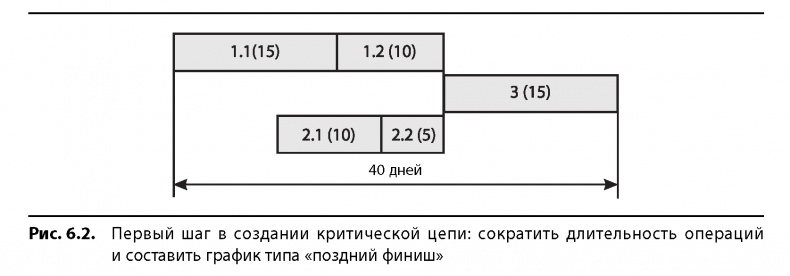
Чертим диаграмму, сдвигая все операции на максимально поздние сроки. В данном случае необходимо лишь добавить ограничение «начало как можно позднее» к операции 2.1.
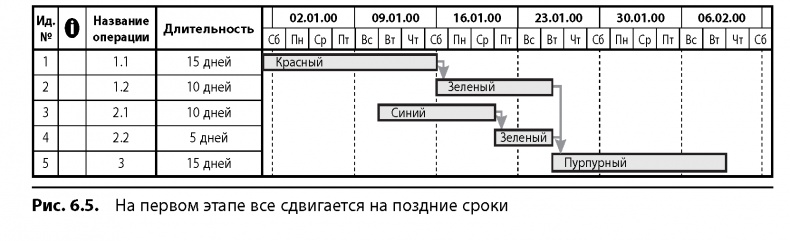
Затем устраняем конфликт ресурсов, двигаясь с конца проекта к началу (рис. 6.5).
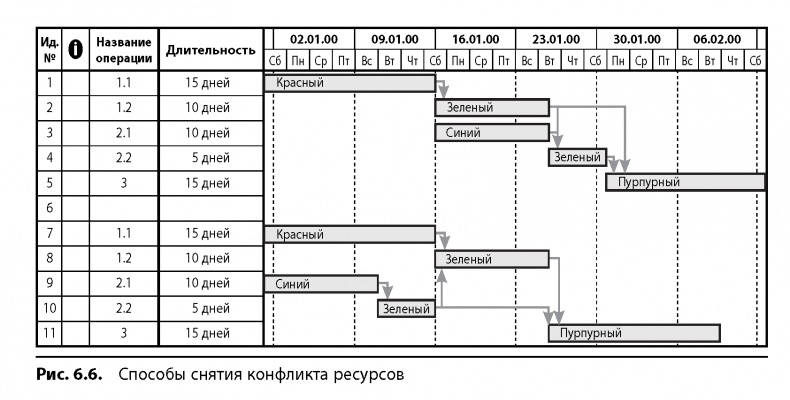
На рис. 6.6 дается два способа снятия конфликта за ресурс «зеленый». Посмотрите, в каждом графике отображается новый тип зависимости от ресурса-ограничения. Какой из способов предпочтительней? На первый взгляд может показаться, что второй — нижний, поскольку последовательность операций получается короче. Во втором случае длина обеих цепочек одинакова, так что любую можно выбрать в качестве критической. А теперь добавьте в оба расписания проектный буфер и буферы на слияние путей и посмотрите, что получится.
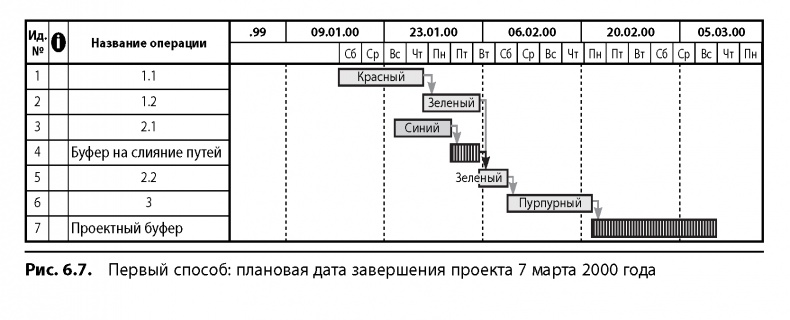
На рис. 6.7 показан план, полученный после применения первого способа снятия борьбы за «зеленый» ресурс. В критическую цепь вошли все операции, кроме операции 2.1. Размер буферов на слияние путей определяем как 50% от общей длительности работ пути, впадающего в критическую цепь.
Какой бы путь из двух мы ни выбрали в качестве критической цепи при первом способе снятия конфликта, общая длительность работ получится одинаковой. Также в обоих случаях после добавления буфера на слияние путей некритическая цепь получается больше критической. Это нормально. Просто появилось дополнительное время для завершения некритических цепочек работ. Обычно так получается, когда имеется два или более путей почти одинаковой длины, но, как правило, в крупных проектах это явление практически не заметно. Двигаемся дальше и устраняем следующий конфликт (рис. 6.8).
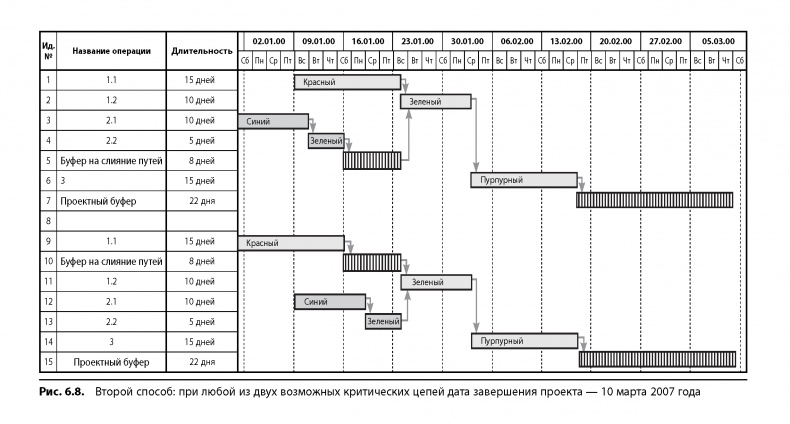
Все из рассмотренных типов расположения работ одинаково годятся в качестве основы для построения плана, поскольку разница между ними по отношению к буферу проекта ничтожно мала. Зачастую можно несколько улучшить ситуацию и снять конфликт, перенеся самую длинную из операций на более поздний срок. Таким образом критическая цепочка останется самой длинной из последовательностей работ, а запас в проектном буфере увеличится, что усилит защиту вашего проекта от влияния общих причин вариабельности.
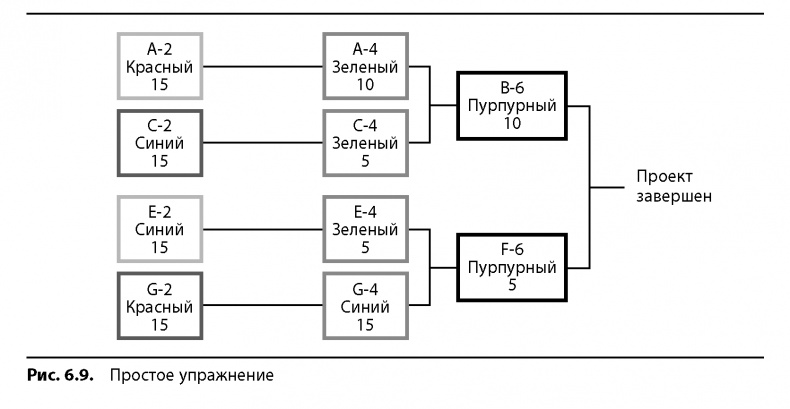
На основе рис. 6.9 постройте план критической цепи со всеми соответствующими буферами. Первая строка в каждом квадратике — номер операции. Вторая — ресурс, обозначенный цветом. Третья — длительность операции в днях (уже сокращенная). (Чтобы проверить приблизительную длительность расписания, которое должно у вас получиться, смотрите последний вопрос раздела 6.10. Учтите: приемлемый вариант критической цепи может отличаться от критического пути лишь на небольшой процент от величины буфера проекта.
6.3.2. СЛОЖНЫЙ ПРИМЕР
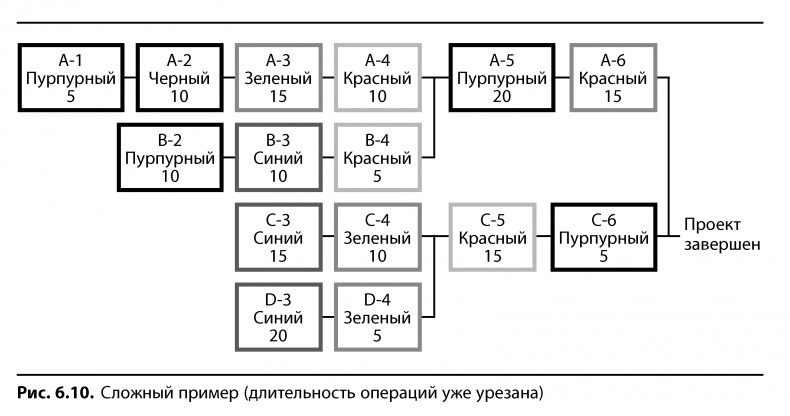
На рис. 6.10 дана диаграмма проектных работ следующего, более сложного примера. Верхняя строка в каждом квадратике — идентификатор операции. Цвет обозначает необходимый тип ресурса. Цифры в нижней строке показывают длительность операции в днях. Длительность взята с 50%-ной вероятностью.
Необходимо составить план этого проекта методом критической цепи.
Первый шаг — начертить график работ. На рис. 6.11 работы представлены в виде диаграммы Гантта, составленной средствами MS Project. Посмотрите диаграмму слева направо и обратите внимание на пересечение операций А-1 и В-2, где исполнителем назначен «пурпурный». Также пересекаются операции В-3, С-3 и D-3, у которых ресурс «синий». Можно легко заметить, что критический путь в этой диаграмме — верхняя цепочка работ, так как в ней нет никаких разрывов.
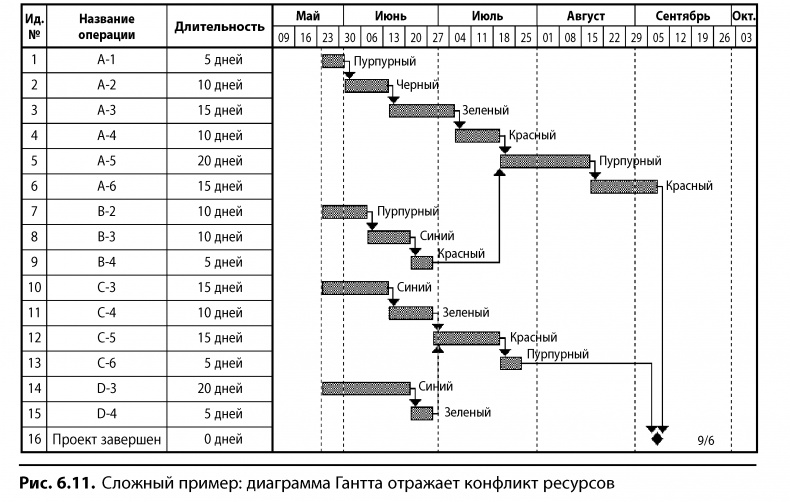
Программа MS Project позволяет снять конфликт путем выравнивания ресурсов, как продемонстрировано на рис. 6.12. Обратите внимание, теперь почти во всех цепочках операций есть пробелы, и поэтому считать их критическим путем нельзя.
Теперь необходимо найти критическую цепь. Рис. 6.13 показывает критическую цепь, определенную при помощи программы ССРМ + . Как вы видите, критическая цепь несколько раз «перепрыгивает» с одной логической последовательности операций на другую. При этом, если смотреть с конца проекта, видно, что на данный момент в критической цепи нет пробелов, хотя они есть почти во всех логических цепочках работ.












