Как и в случае с коэффициентом бета, один из способов – обратиться к истории. В различных базах данных (в Англии исследования «Акции – государственные ценные бумаги» и более современные исследования Лондонской школы бизнеса, в США исследования компании Ibbotson) ежегодно приводятся показатели доходности разных классов ценных бумаг. При этом возникает методический вопрос: должен каждый год рассматриваться как самостоятельная единица и годовая доходность при этом арифметически усредняться или следует весь рассматриваемый период (несколько десятилетий) рассматривать как одну единицу и годовую доходность рассчитывать как среднее геометрическое? Второй вариант представляется более предпочтительным, но и здесь, как в случае с коэффициентом бета, важно, соответствуют ли основанные на исторических данных оценки ожидаемым в будущем параметрам?
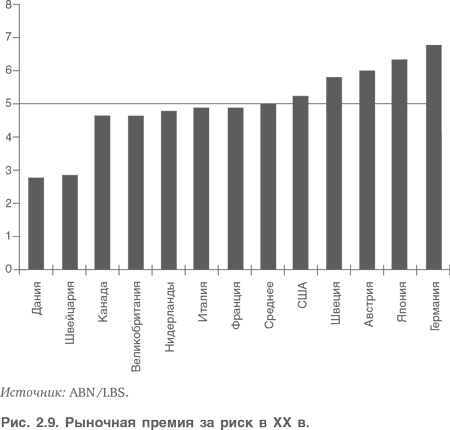
На рис. 2.9 приведены основанные на исторических данных за ХХ в. оценки разницы между значениями годовой доходности акций и долгосрочных государственных облигаций на рынках разных стран. Среднее арифметическое таких разниц составляет около 5 %, т. е. в среднем акции сулят примерно на 5 % бóльшую доходность, чем долговременные государственные облигации за этот период.
Альтернативный подход: рассчитать ожидаемую доходность рынка ценных бумаг путем оценки роста будущих дивидендов. Формула расчета ожидаемой доходности рынка ценных бумаг, полученная простым преобразованием формулы Гордона, выглядит так:
В конце 2003 г. историческая доходность английского индекса акций FT составляла 3,12 %. Эквивалентная прогнозная величина могла составить примерно 3,15 %, многолетний номинальный рост дивидендов можно оценить примерно в 4,5 % в год. Из этого можно заключить, что доходность рынка ценных бумаг Великобритании была на уровне 7,65 %. На ту же дату 10-летняя государственная облигация давала доходность при погашении 4,77 %. Вычитание этой величины из прогнозной доходности дает премию за рыночный риск 2,88 %. Принимая во внимание естественную неточность сделанных прогнозов, разумно принять премию за рыночный риск равной 3 %. Предпринимались многочисленные попытки рассчитать премию за рыночный риск неявным образом, на основе данных разных исторических периодов. Такие расчеты в основном дают значение премии за рыночный риск 3–4 %. Это несколько ниже, чем фактическая премия в ХХ в.
2.5. Комментарии к САРМ
Специалисты часто применяют модель САРМ и не задаются вопросом о ее применимости. Отчасти это объясняется тем, что она достаточно хорошо работает и проста в применении. В тех случаях, когда применение модели не дает удовлетворительного результата – например, в случае венчурных инвестиций в неликвидные активы, – ее игнорируют.
Другие модели приведены ниже. Первая – теория арбитражного ценообразования – вместо предположения о существовании одного фактора, определяющего ожидаемую доходность акции (подверженность рыночному риску), содержит предположение о наборе факторов. Многофакторный подход подразумевает анализ многофакторной регрессии для определения коэффициентов для разных факторов. Одним из факторов обычно является рыночный риск. Такой подход позволяет лучше объяснить исторические цены акций и более точно рассчитать коэффициент бета, однако требует больших затрат времени. К тому же нет достаточных оснований считать, что этот подход позволяет делать более точные прогнозы стоимости капитала по сравнению с прогнозами, построенными с помощью САРМ.
Вторая основана на статистическом исследовании, первоначально проведенном Фамой и Френчем, которое показало, что доходность акций может быть лучше объяснена на основе беты и двух переменных – размера компании и отношения цена / балансовая стоимость. О значении последнего фактора ведутся споры, но, возможно, одно из преимуществ этого подхода в том, что он учитывает ликвидность. Другое исследование показало, что корректировка рыночной цены капитала с учетом размера и финансового рычага повышает способность модели объяснять исторические данные о доходности акций по сравнению с моделью САРМ. Но поскольку коэффициент бета и финансовый рычаг тесно связаны, основное преимущество этого подхода, возможно, такое же, как и у метода Фамы – Френча, – учет ликвидности. На практике, аналитики рынка ценных бумаг используют один из двух подходов: они используют либо стандартный подход САРМ (так поступает большинство), либо ставку дисконтирования, для которой рыночная цена капитала скорректирована с учетом эффекта финансового рычага и уровня ликвидности.
3. Проблема роста
Литературу по вопросам ставки дисконтирования можно разделить на слишком простую и чрезмерно сложную. Отчасти проблема заключается в том, что и практики рынка ценных бумаг, и вся система их подготовки опираются на теорию, которая была разработана Миллером и Модильяни почти полвека назад, при этом более поздние экономические исследования остаются без внимания. Кроме того, все модели, обсуждавшиеся нами выше, представляют собой последовательные вариации на тему одной и той же формулы (поэтому выбор среди моделей сводится к соображениям удобства, а проблемы сводятся к их применимости), а к моделям, описывающим ставку дисконтирования, это не относится. Разные формулы на самом деле подразумевают разное представление о реальном мире, а будучи примененными к одной бухгалтерской отчетности, приводят к разным оценкам. Тем важнее правильно осмыслить эти модели.
Миллер и Модильяни чаще всего вспоминаются в связи с их утверждением, что, если не принимать во внимание налогообложение и риск дефолта, на стоимость компании не влияют ни финансовый рычаг (поскольку инвесторы сами могут управлять своим балансом и определять, какой финансовый рычаг им нужен), ни доля дивидендов в прибыли (поскольку слишком большие распределенные дивиденды сегодня должны быть компенсированы завтра).
На самом деле большое значение в их работе имел вывод, что увеличение финансового рычага влияет на стоимость акционерного капитала. Поскольку стоимость бизнеса не изменяется при изменении финансового рычага (денежный поток 100 долл. в год, который оценивался в 1000 долл., будучи дисконтирован по 10 %, все равно сохраняет стоимость 1000 долл.), оказалось возможным рассчитать, как изменение финансового рычага влияет на стоимость акционерного капитала. В табл. 2.2 показаны годовой денежный поток, ставки дисконтирования и стоимость активов, финансируемых с различным финансовым рычагом, при этом отдельно оценены задолженность, акционерный капитал и капитал компании в целом.

Если изменение финансовой структуры не влияет на стоимость активов, то средневзвешенная стоимость капитала (WACC) не меняется при изменении соотношения заимствований и акционерного капитала. Увеличение доли заемного капитала приводит к росту стоимости уменьшающейся доли акционерного капитала и к возрастанию доли более дешевого заемного капитала в общей стоимости. Средневзвешенная стоимость капитала остается неизменной. На рис. 2.10 показано изменение стоимости акционерного и заемного капитала и средневзвешенной стоимости капитала в условиях роста финансового рычага.

