И вот теперь оказалось, что не только гравитация, но и все прочие физические проявления – лишь следствие геометрии нашего многомерного мира.
Стоп! А что значит «многомерный мир»? И что это все-таки за струны такие геометрические в удивительной теории струн? Отвечу…
Мы не можем сказать, из чего «сделаны» струны, сам вопрос не имеет смысла. Но мы можем описать эти струны, понять, какие они.
Они – одномерные. А пространство, в котором они колеблются, – многомерное.
Непонятно?
Сейчас разберемся. Что такое мерность пространства? Ну, это все знают! А кто не знает, сейчас узнает.
Наше пространство трехмерно. В нем три измерения – длина, ширина и высота. Вы спросите: а как еще может быть? Ну, в теории может быть по-разному. Школьная геометрия, например, изучает, в основном, двумерное пространство. Двумерное пространство – это плоскость. На плоскости есть только два измерения – длина и ширина, высоты нету… Одномерное пространство – линия. В нем только одно измерение – длина… И есть нуль-мерное пространство – точка. Точка – она и есть точка – ни длины в ней, ни ширины, ни высоты…
Можно представить себе некий двумерный мир и живущих в нем плоскатиков, причем ясно, что жизнь у ребят не сахар: им приходится производить выделения из организма через то же самое отверстие, через которое они едят. То есть какают плоскатики через рот. Иначе невозможно: если вы попробуете нарисовать плоскатика в виде «плоской трубы», в один конец которой входит пища (рот), а из другого конца выходит бяка (попа), вы увидите, что ваш плоскатик развалился на две не соединенные друг с другом части. Человеку в этом смысле повезло: в трехмерном мире благодаря высоте тело не разваливается на две части.
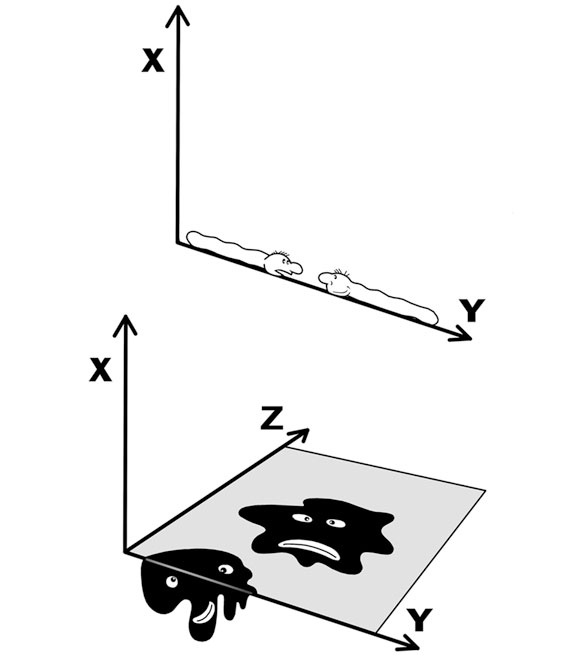
Плохо быть плоскатиком! И линейщиком… Для удобства восприятия у линейных созданий показана некая толщина, чтобы мы их увидели. Но вообще-то поперечного размера не должно быть в одномерном мире.
В одномерном мире ситуация еще хуже – живущие там линейщики не смогли бы даже обойти друг друга, каждый житель этого мира может иметь только двух соседей – одного слева и одного справа.
Пространственное измерение – это перпендикуляр, который можно восстановить к другому измерению. Если к одномерной линии прочертить под углом 90 градусов другую линию (перпендикуляр), получится уже двумерность, то есть плоскость. В плоскость тоже можно воткнуть сверху перпендикуляр – третью координату – получится пространство. В плоскости существуют только плоские фигуры – треугольники, окружности, квадраты… А в пространстве объемные – пирамиды, шары, кубы, конусы… Это все легко себе представить, не так ли?
А вот четырехмерное пространство представить себе никак невозможно – просто потому, что мы не можем выйти за пределы своего трехмерия и воткнуть еще один перпендикуляр так, чтобы он располагался под прямым углом к остальным трем. Некуда его втыкать в нашем мире! Но это не значит, что четырехмерие, пятимерие и так далее не могут существовать.
Могут.
Теоретически. И поэтому в теории струн одномерные, не имеющие толщины струны колеблются в 10-мерном пространстве. Наш мир, получается, десятимерен, если верить теории струн! Почему же мы не видим других измерений, а видим только три? Да потому что остальные измерения свернуты, отвечает теория, они компактифицированы. «Лишние» измерения скручены в такие как бы трубочки, диаметр коих столь мал, что нами не замечается.
Увы, наглядных представлений тут нет. Потому понять это все можно только с помощью математики, оперируя сложными формулами, которые понимают считаные сотни людей на планете. И тут возникает главный вопрос: ну ладно, а почему вообще математика, то есть чистой воды голая придумка человека, правильно описывает реальный мир? Почему мир математичен, то есть подчиняется неким правилам математики, высосанным из пальца? Ведь, повторюсь, математика – это целиком выдуманная наука, состоящая из абстрактных значков. Значки эти и правила, по которым ми можно оперировать, придуманы людьми.
Отчего же природа им подчиняется?
Это величайшая загадка мироздания. Объяснения нет. Но математические и геометрические закономерности (в виде так называемых золотых сечений, например) мы видим везде в природе. Пока что, в какие бы глубины вселенной и микромира мы ни забрались, всюду математика работает. И нет никаких причин полагать, что когда-нибудь она откажет, будучи не в силах описать мир. Более того, среди строгих ученых ходит поговорка о том, что любая наука является наукой лишь настолько, насколько она оперирует математикой. С этой точки зрения история – не наука, литературоведение – не наука, психология – не наука. Ибо нету в них нужной для науки точности, которую привносит в дисциплину математика! Но почему работает сама математика, будучи голой придуманной абстракцией, никто не знает.
Ответа на сей вопрос пока нет. И то, что физика на каких-то самых глубоких уровнях миропознания свелась к геометрии пространства и чистой математике, поражает. Но с другой стороны, а разве могло быть иначе?..



