Поэтому большая часть фантастики близка к действительности, существующей где-то в мультивселенной. Но не вся. Например, нет историй, в которых верны мои рассказы про неисправность телепортатора, потому что они требуют других законов физики. Как нет и историй с другими фундаментальными постоянными, такими как скорость света и заряд электрона. Однако есть смысл, при котором другие законы физики кажутся верными некоторое время в некоторых вариантах истории из-за последовательности «маловероятных случайностей». (Также могут быть вселенные, в которых действуют другие законы физики, что необходимо для антропных объяснениях тонкой настройки. Но пока что жизнеспособной теории для такой мультивселенной нет.)
Представьте себе одиночный фотон, выпущенный коммуникационным лазером звездолёта и движущийся по направлению к Земле. Как и частица космического излучения, в разных историях он попадает в каждую точку её поверхности. В каждой из них фотон поглощается только одним атомом, а остальные изначально совершенно не будут затронуты. Приёмник для такой связи должен тогда обнаруживать относительно большое, дискретное изменение, которое претерпел этот атом. Важное следствие для конструкции измерительных устройств (включая глаза) состоит в том, что как бы далеко ни находится источник, толчок, данный атому пришедшим фотоном, всегда одинаков: просто чем слабее сигнал, тем меньше толчков. Если бы это было не так, например, если бы выполнялись законы классической физики, слабые сигналы гораздо легче тонули бы в случайном местном шуме. Это то же самое, что и преимущество цифровой обработки информации над аналоговой, о котором я говорил в главе 6.
Некоторые мои исследования в области физики имеют отношение к теории квантовых компьютеров. Существуют компьютеры, в которых несущие информацию переменные различными средствами защищены от запутывания с окружением. Это делает возможным новый режим вычислений, в котором поток информации не замкнут в единственной истории. В одном из типов квантового компьютинга огромное число различных вычислений, производимых одновременно, могут влиять друг на друга, а значит, вносить свой вклад в результат. Это так называемый квантовый параллелизм.
В типичном квантовом вычислении отдельные биты информации представляются физическими объектами, называемыми «кубитами» — квантовыми битами, у которых есть большое разнообразие физических реализаций, всегда обладающих двумя важными свойствами. Во-первых, у каждого кубита есть переменная, которая может принимать одно из двух дискретных значений, и, во-вторых, для защиты кубитов от запутывания принимаются особые меры, такие как охлаждение их до температур, близких к абсолютному нулю. Типичный алгоритм, использующий квантовый параллелизм, начинается с того, что вынуждает несущие информацию переменные в некоторых кубитах принять оба значения одновременно. Следовательно, если рассматривать эти кубиты как регистр, представляющий (скажем) число, количество отдельных экземпляров регистра экспоненциально велико: два в степени числа кубитов. Затем некоторое время производятся классические вычисления, и в ходе этого процесса волны дифференциации распространяются на некоторые другие кубиты, но не дальше — благодаря упомянутым особым мерам. Это значит, что информация обрабатывается отдельно в каждой из этих многочисленных автономных историй. Наконец процесс интерференции, включающий все затронутые кубиты, объединяет информацию в этих вариантах в единую историю. Из-за промежуточных вычислений, в которых происходила обработка информации, конечное состояние не совпадает с начальным, как в простом эксперименте с интерференцией, описанном выше (, а представляет собой некоторую его функцию, например
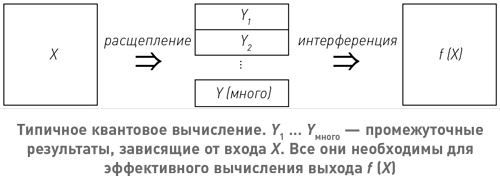
Алгоритм, использующий квантовый параллелизм, делает то же, что и члены экипажа звездолёта, которые могли добиться эффекта большого объёма вычислений, обмениваясь информацией со своими двойниками, вычисляющими ту же самую функцию с разными входными данными. Но если в фантастике эффект ограничен только правилами корабля, которые мы можем придумать в соответствии с сюжетом, то квантовые компьютеры ограничены законами физики, которым подчиняется квантовая интерференция. Таким способом с помощью мультивселенной можно производить только определённые типы параллельных вычислений, для которых математический аппарат квантовой интерференции как раз подходит для сведения в единую историю информации, необходимой для получения конечного результата.
В таких вычислениях квантовый компьютер всего лишь с несколькими сотнями кубитов смог бы в параллельном режиме производить гораздо больше вычислений, чем атомов в видимой части нашей Вселенной. На момент написания этой книги были построены квантовые компьютеры, насчитывающие около десяти кубитов. Дальнейшее «масштабирование» этого подхода — огромной сложности задача для квантовых технологий, но исследователи постепенно приближаются к её решению.
Я уже упоминал, что, когда крупный объект подвергается незначительному воздействию, в результате этот объект обычно остаётся совершенно незатронутым. Теперь я могу объяснить, почему это так. Например, в уже обсуждавшемся интерферометре Маха — Цендера два экземпляра одного фотона проходят по двум различным путям. В ходе этого процесса они отражаются от двух разных зеркал. Интерференция будет иметь место, только если не возникнет запутанности фотона с зеркалами, но она возникнет, если в любом из двух зеркал останется даже самая незначительная запись о столкновении (так как это будет дифференциальный эффект для двух экземпляров фотона, проходящего по двум различным путям). Даже одного кванта изменения амплитуды вибрации зеркала на его опоре, например, будет достаточно, чтобы помешать интерференции (последующему слиянию двух экземпляров фотона).
Когда один из экземпляров фотона отражается от любого из зеркал, у него изменяется импульс, а значит, согласно закону сохранения импульса (который универсально выполняется, как в классической, так и в квантовой физике), импульс зеркала должен измениться на равную и противоположную величину. Поэтому кажется, что в каждом варианте истории после столкновения с фотоном одно зеркало, но не другое, должно вибрировать с немного большей или меньшей энергией. Такое изменение энергии могло бы указывать, по какому пути прошёл фотон, и между зеркалами и фотоном возникла бы запутанность.
К счастью, этого не происходит. Напомню, что на достаточно детальном уровне то, что нам в первом приближении видится как один вариант истории для зеркала, пассивно пребывающего или слегка вибрирующего на опоре, на самом деле представляет собой огромное число историй, в которых экземпляры всех атомов постоянно расщепляются и воссоединяются. В частности, совокупная энергия зеркала принимает огромное число возможных значений в окрестности среднего, «классического». Но что же происходит, когда фотон ударяет по зеркалу, изменяя эту суммарную энергию на один квант?
На минуту упростив ситуацию до предела, представим себе всего пять из бесконечного числа экземпляров зеркала, причём у каждого из них своя энергия колебаний со значением в диапазоне от двух квантов ниже до двух квантов выше среднего. Каждый экземпляр фотона попадает на один экземпляр зеркала и сообщает ему один дополнительный квант энергии. Таким образом, после этого удара средняя энергия экземпляров зеркала увеличится на один квант, и теперь это будут экземпляры со значениями энергии от одного кванта ниже до трёх квантов выше старого среднего. Но поскольку на этом уровне детализации не существует автономных историй, связанных с любым из этих значений энергии, не имеет смысла спрашивать, является ли экземпляр зеркала с конкретным значением энергии после удара тем же, что и тот, у которого раньше была такая энергия. Объективным является только тот физический факт, что из пяти экземпляров зеркала у четырёх значения энергии те же, что были раньше, а у одного — нет. Значит, только он — тот, у которого энергия на три кванта выше, чем предыдущее среднее, — несёт запись о столкновении с фотоном. А это означает, что только в одной пятой вселенных, в которых фотон ударился о зеркало, волна дифференциации дошла до зеркала, и только в них будет подавлена последующая интерференция между экземплярами этого фотона, которые столкнулись или не столкнулись с зеркалом.



