Это универсальная система счёта. Но, аналогично уровням эмерджентности, у универсальности тоже есть иерархия. Следующий уровень после счёта «палочками» — счёт, в котором задействована специальная запись числа. В первом случае, отмечая, сколько коз пришло или ушло, человек думает просто «ещё одна, ещё одна и ещё одна», а считая их, он проговаривает про себя «сорок, сорок одна, сорок две…».
Только задним числом мы можем рассматривать «палочки» как систему счисления и называть её «унарной» («единичной»), и как таковая эта система непрактична. Например, даже простейшие операции с числами, представленными чёрточками, такие как сравнение, арифметические операции и даже просто копирование, влекут за собой повторение всего процесса. Если у вас было сорок коз, вы продали двадцать и отметили оба этих действия с помощью чёрточек, вам всё равно придётся произвести двадцать отдельных операций удаления, чтобы записи соответствовали действительности. Аналогично, чтобы проверить, совпадают ли две сходные на вид записи, пришлось бы вычерчивать их друг под другом и сличать. Поэтому люди начали совершенствовать систему. Наверно, раньше всего придумали просто группировать чёрточки — например, писать
 вместо ||||||||||. Так сравнивать числа и проводить арифметические операции стало проще, поскольку можно было записывать целые группы и сразу видеть, что
вместо ||||||||||. Так сравнивать числа и проводить арифметические операции стало проще, поскольку можно было записывать целые группы и сразу видеть, что
 отличается от
отличается от
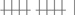 . Позднее и для самих этих групп были подобраны более короткие условные символы: в древнеримской системе использовались символы типа I, V, X,
. Позднее и для самих этих групп были подобраны более короткие условные символы: в древнеримской системе использовались символы типа I, V, X,
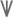 , C,
, C, D, и CD для обозначения одного, пяти, десяти, пятидесяти, сотни, пяти сотен и тысячи. (Как видите, это не совсем те «римские цифры», которые мы используем сегодня.)
Это ещё один случай постепенного совершенствования, направленного на решение специфических, обывательских проблем. И снова, по-видимому, никто к большему и не стремился. Хотя добавлением простых правил можно было сделать систему гораздо более функциональной, и даже несмотря на то, что римляне действительно время от времени добавляли некоторые из таких правил, они делали это, не стремясь к универсальности и не достигая её. На протяжении нескольких столетий в этой системе правила были следующие.
— Размещённые рядом символы складываются. (Это правило унаследовано от системы подсчёта «палочек».)
— Символы записываются слева направо в порядке убывания их величины.
— Когда это возможно, смежные символы следует заменять одним, отражающим их суммарное значение.
(Правило вычитания, присутствующее в современной римской системе счисления, по которому IV означает четыре, было введено позже.) Второе и третье правило гарантируют единственность представления каждого числа, что сильно упрощает сравнение. Без этих правил могли бы существовать и XIXIXIXIXIX, и VXVXVXVXV, и никто не мог бы с первого взгляда сказать, что это одно и то же число.
За счёт применения универсальных законов сложения эти правила давали системе одно важное преимущество над подсчётом с помощью «палочек», а именно возможность производить арифметические операции. Например, возьмём числа семь (VII) и восемь (VIII). Согласно правилам поместить их друг за другом VIIVIII — всё равно что сложить их. Затем по правилам нужно переставить символы в порядке убывания их величины: VVIIIII. Затем нужно заменить две V на X и пять I на V. В результате получим XV, что является представлением числа пятнадцать. Но при этом происходит нечто новое, и дело не просто в сокращении записи: открыта и доказана абстрактная истина, связывающая между собой семь, восемь и пятнадцать, и при этом никто ничего не отмечал и не пересчитывал. Мы работали с самими числами, посредством их записей.
Когда я говорю, что арифметические операции совершались системой записи чисел, я вкладываю в это буквальный смысл. Конечно, физически эти преобразования производили люди, пользовавшиеся этой системой. Но для этого им сначала нужно было записать её правила у себя в голове, а затем выполнить их, как компьютер выполняет программу. Причём, как известно, именно программа диктует действия компьютеру, а не наоборот. Значит, процесс, которые мы называем «выполнением арифметических операций с римскими цифрами» также состоит в том, что римская система записи использует нас для совершения арифметических операций.
Римская система смогла выжить только за счёт того, что вынуждала людей совершать эти действия, другими словами, она добивалась того, что римляне копировали её из поколения в поколение: они считали её полезной и передавали своим потомкам. Как я сказал, знания — это информация, которая, физически закрепившись в подходящей среде, стремится там остаться.
Услышав, что римская система записи чисел подчиняет нас себе, чтобы размножиться и не прекратить своё существование, кто-то, наверно, может подумать, что люди низводятся до статуса рабов. Но это было бы заблуждением. Люди состоят из абстрактной информации, включая характерные идеи, теории, намерения, чувства и другие состояния души, которые характеризуют конкретное «я». Спорить с тем, что, когда мы находим римские цифры полезными, мы идём у них «на поводу», всё равно что протестовать против того, что мы ходим на поводу у наших намерений. Рассуждая таким образом, можно прийти к тому, что пытаться спастись от рабства — это тоже рабство. На самом же деле, когда я говорю, что подчиняюсь программе, которая меня же составляет, (или что я подчиняюсь законам физики), в слово «подчиняться» я вкладываю несколько иной смысл, чем раб. Эти два значения слова объясняют события, находящиеся на разных уровнях эмерджентности.
Вопреки тому, что иногда говорят, существовали и достаточно продуктивные способы умножения и деления римских чисел. Так, можно было узнать, что корабль, в трюме которого — XX ящиков, в каждом из которых V рядов по VII кувшинов, всего перевозит DCC кувшинов, и при этом длинных вычислений, подразумеваемых в этом числе, не потребуется. И можно было сразу сказать, что DCC меньше, чем DCCI. Таким образом, возможность управляться с числами без начертания и подсчёта «палочек» позволяла вычислять цены, зарплаты, налоги, проценты по кредиту и так далее. Кроме того, это было концептуальным продвижением, открывшим двери будущему прогрессу. Однако в том, что касается этих более сложных применений, система универсальной не была. Поскольку символа со значением, большим CD (одна тысяча), не было, все числа, начиная с двух тысяч, начинались с цепочки из нескольких CD, тем самым становясь всего лишь условными метками со значением тысячи. Чем больше их было в числе, тем больше для выполнения арифметических операций приходилось прибегать к старой системе меток (рассматривать множество одинаковых символов друг за другом).



 вместо ||||||||||. Так сравнивать числа и проводить арифметические операции стало проще, поскольку можно было записывать целые группы и сразу видеть, что
вместо ||||||||||. Так сравнивать числа и проводить арифметические операции стало проще, поскольку можно было записывать целые группы и сразу видеть, что
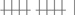 . Позднее и для самих этих групп были подобраны более короткие условные символы: в древнеримской системе использовались символы типа I, V, X,
. Позднее и для самих этих групп были подобраны более короткие условные символы: в древнеримской системе использовались символы типа I, V, X,
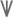 , C,
, C,