Тем не менее, независимо от того, считать ли тонкую настройку видимым признаком замысла или нет, она ставит правомерную и важную научную проблему, и вот почему. Если правда в том, что природные константы не подогнаны с целью создать в итоге жизнь, а большая часть незначительных их вариаций всё же допускает то или иное развитие жизни и разума, хотя и в совершенно иной среде, то это будет необъяснимой природной закономерностью, а значит — проблемой, за которую может взяться наука.
Если же законы физики действительно тонко настроены, как это представляется нам сегодня, то есть две возможности: либо эти законы — единственные воплощённые в реальности (как вселенные), либо есть другие области реальности — параллельные вселенные
[21] — с другими законами. В первом случае нужно ожидать, что имеется объяснение того, почему законы такие, какие они есть, и оно либо будет ссылаться на существование жизни, либо нет. Если будет, то мы окажемся отброшены назад к проблеме Пейли: тогда получится, что эти законы имели «видимые признаки замысла» по созданию жизни, а не эволюционировали. Если же объяснение не будет ссылаться на существование жизни, то останется необъяснённым другой вопрос: раз законы таковы, как они есть, по причинам, не связанным с жизнью, то почему они настроены так, что она создаётся?
Если есть много параллельных вселенных, каждая со своими законами физики, и в большинстве из них невозможна жизнь, то можно полагать, что наблюдаемая тонкая настройка — лишь следствие парохиальной перспективы. Только во вселенных, населённых астрофизиками, может возникнуть вопрос о том, почему константы кажутся тонко настроенными. Такой ход объяснения известен как «антропная аргументация». Считается, что она опирается на так называемый «слабый антропный принцип», хотя, вообще говоря, никакого принципа тут не требуется — только логика. (Уточнение «слабый» нужно из-за того, что было предложено несколько вариантов антропного принципа, представляющих собой нечто большее, чем просто логику, но здесь нет нужды их касаться.)
Однако при тщательном рассмотрении оказывается, что антропных доводов недостаточно для полного объяснения. Чтобы понять, почему это так, рассмотрим аргумент физика Денниса Сиама
[22].
Представьте, что в какой-то момент в будущем теоретики вычислили область значений одной из этих физических констант, при которых существует разумная вероятность появления астрофизиков (любого подходящего типа). Пусть это будет диапазон
[23] от 137 до 138. (Конечно, в действительности числа вряд ли будут целыми, но мы не станем усложнять рассуждения.) Кроме того, подсчитано, что наибольшая вероятность появления астрофизиков соответствует середине диапазона, то есть значению константы 137,5.
Далее экспериментаторы приступили к непосредственному измерению константы, скажем, в лабораториях или путём астрономических наблюдений. Что они должны предсказывать? Весьма любопытно, но из антропного объяснения непосредственно следует предсказание, что значение константы не будет в точности равно 137,5. Почему? Допустим противное. Пусть — по аналогии — центр мишени для дротиков представляет значения, при которых астрофизики могут возникнуть. Будет ошибкой предсказать, что среднестатистический дротик попадёт точно в центр. Аналогичным образом в подавляющем большинстве вселенных, в которых могли бы производиться эти измерения (потому что там есть астрофизики), эта константа не примет в точности значение, оптимальное для образования астрофизиков, и не будет слишком близка к нему в сравнении с размером центра мишени.
Из этого Сиама сделал вывод, что, если бы мы действительно измерили одну из тех физических констант и выяснили, что она очень близка к оптимальной для появления астрофизиков, это бы статистически опровергло, а не подтвердило антропное объяснение её значения. Конечно, остаётся возможность, что это просто совпадение, но если бы мы согласились принимать в качестве объяснений астрономически невероятные совпадения, то нам вообще не следовало озадачиваться проблемой тонкой настройки, а мистеру Пейли мы должны были бы сказать, что часы на пустыре могли образоваться сами собой.
Более того, во вселенных, где условия настолько враждебны, что едва допускают появление астрофизиков, их существование должно быть относительно маловероятным. Если выстроить все значения, согласующиеся с появлением астрофизиков, в ряд, то исходя из антропного объяснения мы будем ожидать, что измеренное значение попадёт в какую-нибудь типичную точку, не очень близко к середине или любому из концов.
Однако — и здесь мы приходим к главному выводу Сиамы — это предсказание кардинально меняется, если объяснить нужно сразу несколько констант. Да, маловероятно, что любая из констант окажется у края своей области значений, но чем констант больше, тем более вероятно, что по крайней мере одна из них там будет. Это можно проиллюстрировать графически следующим образом, заменив центр мишени отрезком прямой, квадратом, кубом… Можно представить себе дальнейший рост числа размерностей, соответствующий количеству тонко настроенных констант. Произвольно определим понятие «у края» как «не далее чем в 10 % от края по отношению ко всей области значений». В случае одной константы, как показано на диаграмме, 20 % возможных значений лежат около одного из краёв области значений, а 80 % — «далеко от края». Но если констант две, то, чтобы оказаться «далеко от края», два значения должны удовлетворять двум ограничениям, и таких пар будет уже только 64 %, а 36 % находятся у края хотя бы по одному из двух измерений. Если констант три, у края лежит уже почти половина вариантов — 48,8 %, если быть точным. А если их 100, то у края окажутся 99,9999999 %!
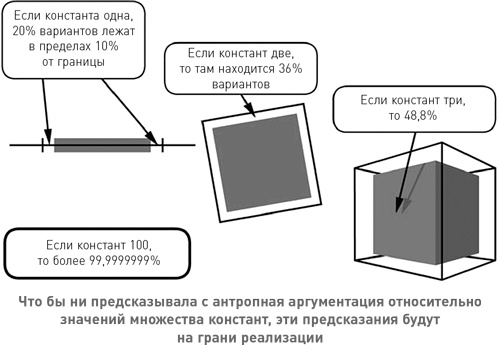
Таким образом, чем больше констант, тем ближе типичная вселенная с астрофизиками к тому, что астрофизиков в ней нет. Число таких констант неизвестно, но, по-видимому, их несколько, и в этом случае подавляющее большинство вселенных в антропно выделенной области будет располагаться вблизи её края. Значит, заключил Сиама, антропное объяснение предсказывает, что Вселенная едва-едва способна производить астрофизиков, — и это предсказание практически противоположно тому, которое делается в случае одной константы!



