Чтобы понять эту идею, необходимо рассмотреть энергетические отношения между Землей, Луной, Марсом и главным поясом астероидов. Пояс астероидов вступает здесь в игру, потому что, как известно, содержит обширные запасы очень богатых металлических руд в условиях низкой гравитации, что делает их потенциально легкими для экспорта на Землю [36]. Например, Джон Льюис из Университета штата Аризона рассмотрел случай простого астероида диаметром всего один километр. Масса такого астероида составит всего 2 миллиарда тонн, из которых 200 миллионов тонн будут приходиться на долю железа, 30 миллионов тонн – высококачественного никеля, 1,5 миллиона тонн – стратегически важного кобальта и 7500 тонн – смеси металлов платиновой группы, средняя стоимость которой при современных ценах может достигать 20 000 долларов за килограмм. В сумме это составит 150 миллиардов долларов для одной только платины. В этом почти нет сомнений, так как у нас имеется много образцов астероидов в виде метеоритов. Как правило, метеоритное железо содержит от 6 до 30 % никеля, от 0,5 до 1 % кобальта и концентрацию металлов платиновой группы по меньшей мере в 10 раз выше, чем в земных рудах. Более того, так как астероиды также содержат немало углерода и кислорода, все эти вещества могут быть выделены из астероида и отделены друг от друга с использованием химических процессов на базе моноокисида углерода, которые мы обсудили в главе 7 для очищения металлов на Марсе. На сегодня известно около 5000 астероидов, из которых около 98 % находятся в главном поясе между Марсом и Юпитером на среднем расстоянии от Солнца примерно 2,7 астрономической единицы, или а.е. (Земля находится на расстоянии 1 а.е. от Солнца). Эта группа в главном поясе включает все известные астероиды, находящиеся в пределах орбиты Юпитера, с диаметрами более 10 километров, сотни диаметром 100 километров и одно тело – Цереру – с диаметром около 950 километров. За исключением некоторого количества мелких объектов, которые подходят к Солнцу ближе, чем Земля, и нескольких замеченных за Юпитером, остальные 2 % астероидов, все малого размера, имеют орбиты, лежащие между орбитами Земли и Марса. Однако число околоземных астероидов, соответствующее 2 % от общего количества, является сильно завышенным в сравнении с количеством астероидов главного пояса, так как относительная близость первых к Земле и Солнцу делает их гораздо более удобными для обнаружения. Разумная оценка будет примерно такой: астероиды главного пояса превосходят по численности околоземную группу по меньшей мере в тысячу раз. Из близких к Земле астероидов около 90 % располагаются ближе к Марсу чем к Земле.
Из примера Льюиса должно стать ясно то, что все эти астероиды вместе представляют огромный экономический потенциал. Хотя в последнее время было сделано многое, чтобы подчеркнуть важность астероидов околоземной группы (особенно в связи с постепенным осознанием того, что, если мы не будем развивать космические программы по защите от таких астероидов, один из них, скорее всего, когда-нибудь врежется в нашу планету и уничтожит человеческую расу), относительные количества астероидов в двух классах с очевидностью показывают, что добыча будет сосредоточена в главном поясе.
Шахтеры, работающие на астероидах, не смогут производить большую часть необходимого им продовольствия на месте. Таким образом, возникнет потребность в импорте продуктов питания и других необходимых товаров или с Земли, или с Марса. Как показано в табл. 8.1 ниже, у Марса в этом отношении будет масса преимуществ. Они связаны с тем, что значения ΔV для запуска реактивной ракеты с Марса гораздо меньше, чем для запуска с Земли, и как следствие, отношение масс (полная масса заправленного космического корабля, деленная на его сухую массу), которое требуется для космических аппаратов, покидающих Марс, также намного меньше.
В таблице 8.1 в качестве примера рассматривается Церера, крупнейший астероид,
[29] расположенный самом центре главного пояса. Однако вы заметите, что я также упоминаю Луну как потенциальный порт назначения. Несмотря на то что она намного ближе к Земле, с точки зрения реактивного движения, гораздо легче достичь Луны с Марса! Для такого запуска требуется отношение масс всего в 12,5, в то время как для полета с Земли на Луну это отношение должно составлять 57,6. И по той же причине путешествия с Земли или с Марса практически на любой околоземный астероид будут менее удобными, чем к астероидам основной группы главного пояса.
Таблица 8.1. Перелеты во внутренней Солнечной системе
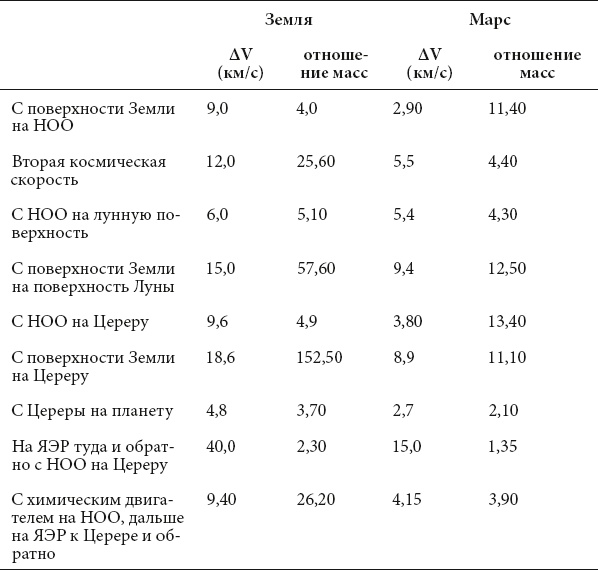
Все строки в табл. 8.1, за исключением последних двух, рассчитаны для системы транспортировки с метаново-кислородными (СН4/O2) двигателями с удельным импульсом в 380 секунд и ΔV, подходящими для траекторий с использованием высокоэффективных химических двигательных установок. Они были выбраны потому, что смесь метана и кислорода обладает самым высоким удельным импульсом из всех видов топлива, которые можно хранить в космосе, и ее можно изготовить на Земле, на Марсе или на углеродистом астероиде. Топливо из смеси водорода и кислорода хоть и имеет более высокий удельный импульс (450 секунд), не может долго храниться в космосе. Более того, оно непригодно для дешевых многоразовых космических транспортных систем, поскольку его стоимость почти на порядок выше, чем для смеси метана и кислорода, и его объемность затрудняет транспортировку топлива на орбиту, если применять многоразовые одноступенчатые ракеты РОСД (но это позволяет использовать его для действительно недорогих ракет для доставки с Земли на НОО). Последние две записи в таблице рассчитаны для ядерных электрических ракет (ЯЭР): для движения в космосе предлагается аргонное топливо с удельным импульсом в 5 тысяч секунд, доступное и на Земле, и на Марсе, а для запуска с поверхности к НОО – смесь метана и кислорода. Такие системы РОСД и ЯЭР, хотя и кажутся сегодня фантастикой, в будущем обещают стать надежной основой для технологии межпланетных перевозок.
Можно видеть, что, если использовать исключительно химические системы двигателей, то отношение масс, необходимое для того, чтобы доставить сухую массу к поясу астероидов с Земли, в 14 раз больше, чем если производить запуск с Марса. Это означает, что при полете с Марса на Цереру отношение массы полезной нагрузки к взлетной массе ракеты по-прежнему гораздо больше, чем при полете с Земли на Цереру. На самом деле расчеты в табл. 8.1 позволяют сделать вывод, что выгодная торговля между Землей и Церерой (или любым другим телом в главном поясе астероидов) с использованием химических двигателей скорее всего невозможна, тогда как между Марсом и Церерой организовать ее не составит большого труда. Так что из таблицы видно, что отношение масс для доставки грузов с Марса на Луну почти в пять раз выше, чем для полетов с Земли на Луну.



