
Рис. 8.4. Пример объяснения бессонницы методом комбинирования взаимосвязей на уровне типа с информацией на уровне токена с ранжированием причин
Разделение типа и токена
Скажем, мы выявили набор факторов, определяющих результативность в баскетболе. Когда однажды в субботу днем во время матча игрок бросает мяч, все факторы наличествуют, однако в последнюю минуту он пролетает мимо сетки, потому что случается землетрясение. Таким образом, имеют место все факторы, которые должны обеспечить попадание мяча в корзину, но этого не происходит. Условия не стали причиной гола (потому что его не было), но, если не брать в расчет землетрясение, другие факторы также не могли стать причиной того, что игрок промазал.
Заметим, что до сих пор мы в основном сосредоточивались на объяснениях, почему произошли события, которые на самом деле произошли. В психологической литературе (см. главу 2) приводится курьезный постулат: людям можно поставить в вину то, чего в действительности не было. Кого-то обвиняют в попытке совершения убийства, а студент, пробовавший списать на экзамене, все равно виновен, даже если его дерзание провалилось.
Если кто-то не полил цветок, а растение все равно выжило, как это можно объяснить? Здесь мы привлекаем внимание к тому, что цветок должен был завянуть, но в реальности не погиб. Отсутствие воды предшествовало, но не стало причиной выживания. Шансы цветка начали снижаться с первого дня, когда он перестал получать воду, и продолжали таять с течением времени. Интуитивно можно понять: когда нечто случается даже при свершении события, снижающего его вероятность, это нечто случается несмотря на, а не в результате этого события. Аналогично, если нечто не произошло несмотря на некое событие, повысившее его вероятность, оно также не произошло, несмотря на событие. К примеру, пациент умер, несмотря на отличный медицинский уход.
Скажем, Адам и Бетти больны гриппом. За неделю до того у Адама был обед с Клер, а та заболевает гриппом через день после второго обеда, с Бетти. Шансы на то, что Клер заболеет гриппом, росли после ее встречи с Адамом, но потом стали снижаться, когда наступил инкубационный период. Они возросли снова после обеда с Бетти и оставались высокими, пока та на самом деле не заболела. Это показано на рис. 8.5.
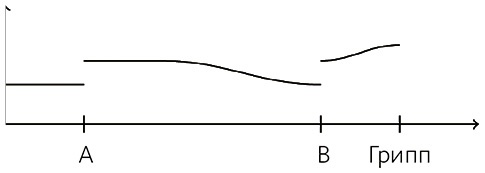
Рис. 8.5. Вероятность гриппа с течением времени. Шанс растет после первого обеда и снижается до второго. После второго контакта вероятность растет то того, пока человек действительно не заболевает гриппом
Несмотря на то что перед нами два примера причины-типа (контакт с носителем гриппа), мы видим, что здесь нет сверхдетерминированности, поскольку только один контакт стал причиной болезни. В предыдущем разделе мы разбирались с подобной ситуацией с помощью временных паттернов на уровне типа. Этот подход имеет отличия, поскольку здесь мы анализируем изменение вероятности на уровне токена. Это также поможет разобраться со случаями, где токен-вероятность отличается от вероятности-типа.
Известно, что вакцины в целом предотвращают летальный исход, но в некоторых редких случаях становятся его причиной; конкретное растение может погибнуть, если его полить кофе, даже если никакое другое растение от этого не погибало; можно возложить вину на человека, попытавшегося совершить убийство, даже если потенциальная жертва выжила. Ключевое ограничение в следующем: исходя из общей информации для объяснения конкретных случаев, мы допускаем, что значимость на уровне типа равна значимости на уровне токена.
Этот подход – посмотреть, как вероятность события меняется после наступления причины и как меняется со временем, – предложил философ Эллери Иллс
[332]. Проблема гораздо шире, чем наши возможности ее рассмотрения на этих страницах, однако суть подхода в том, что единичные вероятности трактуются иначе, чем общие, и в основе лежит изменение вероятности реального события с течением времени.
Использование вероятностей единичного случая, который мы пытаемся объяснить, означает, что мы можем провести различие между тем, что случается как правило, и тем, что случилось в действительности. Здесь по-прежнему учитывается причина, обычно предшествующая событию и влекущая его за собой.
Немаловажно, что при этом мы можем обновить аналитические выводы, приведя их в соответствие с тем, что наблюдаем. В одном из примеров Иллса озорные белки любили отталкивать мячи для гольфа от лунок, но однажды зверек помог игроку, направив мяч прямо в лунку. Если применить метод, основанный на вероятностях уровня типа, то, даже если мы в действительности видим, что траектория мяча делает попадание все более и более вероятным, и наблюдаем, как меняется его путь после того, как по нему ударили, мы все равно не сможем откорректировать уже имеющееся знание на уровне типа, чтобы учесть новые данные. И это приведет к получению не связанных между собой и контринтуитивных результатов.
Когда вероятность меняется после наступления события, становится высокой и остается такой, пока не случится следствие, говорят, что следствие произошло из-за причины. Наоборот, если вероятность события падает после наступления события, тогда следствие происходит, несмотря на событие
[333]. Трудности, характерные для этого подхода, имеют в основном практическую природу, поскольку, к примеру, непросто выяснить вероятность попадания мяча в лунку на каждой точке его траектории.
Автоматизация объяснения
Какими возможностями мы располагаем, чтобы протестировать контрфактуальные рассуждения? Как узнать, насколько изменилась вероятность со временем?
Одно из ограничений в целом многообещающих философских теорий состоит в том, что они, реально учитывая разницу между типом и токеном, требуют наличия порой невозможного количества информации о рассматриваемой ситуации. Да, хорошо знать, что в некий момент времени вероятность попадания мяча в лунку для гольфа составляла 0,5, а после удара по мячу возросла до 0,7. Но откуда взять такие данные?
Один из способов решения проблемы – построение модели интересующей нас системы. Взяв за основу простые законы физики и допущения о скорости ветра и вероятностях прочих действующих факторов, можно предсказать физическую траекторию мяча для гольфа до и после удара. Поскольку исход бывает не детерминирован, можно смоделировать ситуации для каждого положения мяча и рассчитать, как часто он будет оказываться в лунке с конкретной точки.




