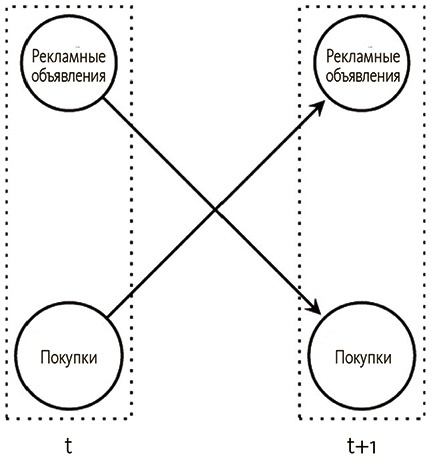
Затем эта структура неоднократно повторится во времени, так что каждый раз покупка будет зависеть от значения рекламы в предыдущий раз, и наоборот.
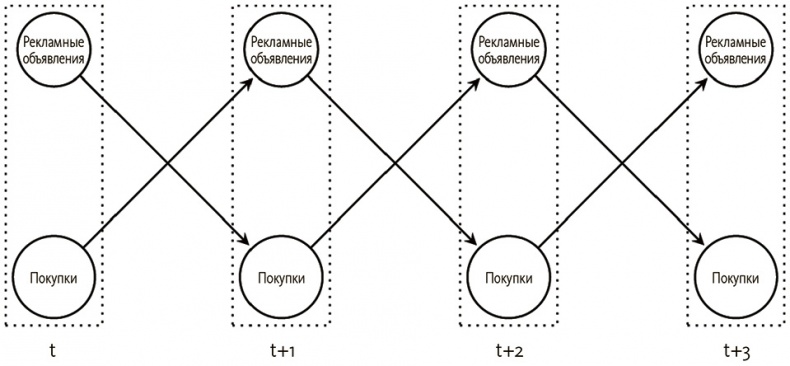
Такой граф называется динамической байесовской сетью, хотя сама структура фактически неизменна во времени
[242].
Возможны более сложные структуры со множественными задержками по времени, и необязательна связь со следующим моментом на временной шкале. Задержки могут быть и более долгими (например, запаздывание между подверженностью вирусу и развитием симптомов). Главное возражение – сложность осмысления таких структур существенно возрастает по мере увеличения числа переменных и задержек по времени.
Когда графическая модель становится каузальной
Мы можем использовать графы для представления причинно-следственных связей, но это не значит, что каждый граф, который мы создаем или о котором узнаём, имеет характер причинности. До сих пор мы всего лишь изображали, как вероятность одной вещи зависит от вероятности другой. Мы могли с такой же легкостью получить графы, показывающие, как перейти от аудиохарактеристик к распознаванию речи, фильтровать спам на основе его содержания и идентифицировать лица на изображениях. Может существовать множество графов, соответствующих набору вероятностных отношений (то есть представляющих тот же набор зависимостей).
Так как же узнать, каузальна ли графическая модель? Ответ кроется прежде всего в допущениях, связывающих графы с теориями, о которых мы уже говорили.
Первые графические модели причинных умозаключений были разработаны философами (Спиретс и др.) и специалистом по информационным технологиям (Перл), которые объединили философию причинности с графическими моделями. Скажем, реклама есть причина одновременно покупок и узнаваемости бренда, как на рис. 6.4 (а). Если бы у нас не было переменной, представляющей рекламные объявления, и мы пытались вывести зависимости из набора данных, то обнаружили бы граф на рис. 6.4 (б), где некорректно показаны покупки в качестве причины узнаваемости бренда.
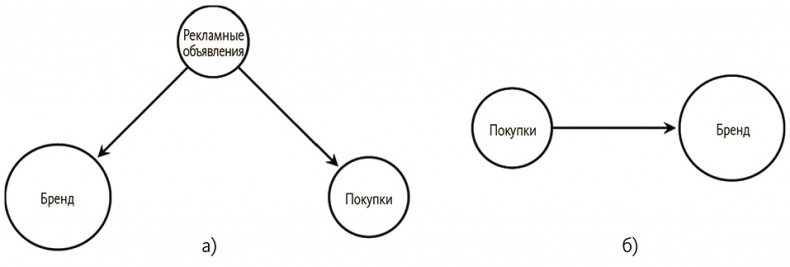
Рис. 6.4. Истинная структура показана слева. Если реклама не наблюдаемая переменная, может появиться некорректная структура справа
Вспомните допущение об отсутствии скрытых общих причин, или о каузальной достаточности, из начала этой главы. Она необходима, чтобы избежать подобных ошибок. В целом может присутствовать общая причина любого ряда переменных, и, если она не измерена, мы не можем быть уверены, что результирующие выводы о каузальности окажутся корректны.
А что будет, если наша рекламная переменная указывает, действительно ли было куплено рекламное время на ТВ, но истинная причина – это просмотр рекламы определенное количество раз?
Как уже говорилось, нам нужны правильные переменные. Каузальные взаимосвязи могут включать в себя сложные их наборы: если выкурить одну сигарету, это вряд ли приведет к раку легких, но многолетнее курение – уже более сильная причина; лекарства часто имеют порог токсичности, так что 5 мг препарата могут не вызвать опасных последствий, а вот 50 мг – уже смертельная доза; грейпфрут не вреден, но он взаимодействует со многими лекарствами, вызывая серьезные побочные эффекты. Если к числу переменных относится факт курения (а не его продолжительность), факт приема лекарства (а не доза) и потребление грейпфрутов (а не их потребление на фоне приема определенного лекарства), то можно не найти причинных зависимостей или определить их неверно.
Такие структуры представляют собой вероятностные отношения и сообщают, какие переменные необходимы для прогнозирования значения остальных, однако для фактического расчета вероятности требуется еще один элемент информации.
Байесовская сеть состоит из двух частей: это структура (то есть как именно связаны между собой переменные) и набор распределения условных вероятностей. Если не слишком вдаваться в детали, это всего лишь таблицы, которые позволяют узнать вероятность каждого значения переменной, исходя из значений ее причин. Для простого графа с рекламой и покупкой хватит двух рядов и двух колонок.
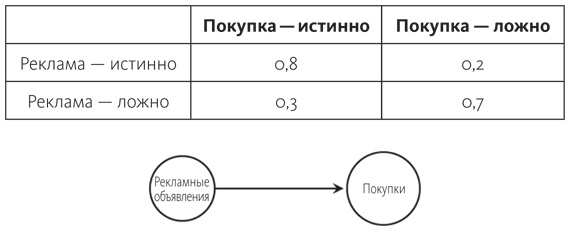
Сумма каждого ряда составляет 1, поскольку, независимо от значений, которые принимает реклама, покупка также должна иметь некое значение, а сумма вероятностей равняться 1. Колонки не суммируются до единицы, потому что они дают вероятность конкретного значения покупки при условии двух значений рекламы. Наш простой граф не завершен, так как для него нужна еще одна таблица с вероятностью рекламы. То есть теперь известно, как определить вероятность покупки с учетом значения рекламы; но как выяснить вероятность рекламы? В этой таблице будет только два числа, поскольку у рекламы в графе нет родительских переменных, и ее вероятность ни от чего не зависит (точно так же вероятность того, что бросок монеты будет иметь конкретное значение, обычно не зависит от значения другой переменной).
Для каждого узла в сети мы получим аналогичную таблицу. Знание структуры существенно упрощает расчеты, так как значение каждой переменной задается ее исходными переменными. Напротив, если мы ничего не знаем о связи между переменными, нам придется включить их все в каждую строку таблицы. Если есть N переменных, которые могут быть истинными или ложными, количество строк будет равняться 2N. Мы можем получить знание о структуре и вероятностях из имеющихся данных или создать структуру на основе уже известного и отсюда выяснить вероятности.
В обоих случаях, однако, мы должны быть уверены, что данные корректно представляют истинные зависимости между переменными. Это возвращает к допущению о репрезентативном распределении, или верности. К примеру, мы не получим варианта, когда реклама способствует покупкам только в одном направлении, но мешает, если они ведут, скажем, к усталости от принятия решений. Если такое случится, мы можем не увидеть зависимости между рекламой и покупками, даже если это присутствует в истинной структуре. Мы также можем не найти правильных вероятностей, если на графе мало точек.
Верность может не иметь места в ряде других случаев, например при парадоксе Симпсона. Или когда в зависимости от разделения данных (например, все пациенты против только мужчин или только женщин) мы могли наблюдать независимость, а в действительности ее не было (например, больше женщин принимали лекарство А, чем лекарство B) и результаты отличались (например, у женщин были лучше, чем у мужчин, независимо от лекарства).






