Получается, коэффициент корреляции Пирсона показывает, как варьируются вместе две переменные по сравнению с индивидуальными модуляциями (эти две меры называются «ковариация» и «вариация»). К примеру, мы можем отметить, сколько часов студенты в некой группе проводят за подготовкой к заключительному экзамену, чтобы посмотреть на соотношение показателей. Зная о наборе экзаменационных баллов и количестве часов, проведенных за подготовкой, но не имея возможности сопоставить итоговые оценки и соответствующие временные показатели, мы не определим, есть ли между ними корреляция. В этом случае получится наблюдать индивидуальные вариации каждой переменной, но не их взаимоизменения. То есть мы не можем выяснить, действительно ли большее время, потраченное на занятия, сопровождается более высокими оценками.
Без вариации нет корреляции
Скажем, вы хотите узнать, как получить грант, поэтому спрашиваете всех друзей, которые его имеют, что, по их мнению, помогло им. Все кандидаты оформляли заявку шрифтом Times New Roman; согласно мнению половины, важно, чтобы на каждой странице была как минимум одна иллюстрация; а треть рекомендуют представить заявку за 24 часа до установленного срока.
Означает ли это, что есть корреляция между названными условиями и получением гранта? Нет, не означает, потому что, не видя вариации исходного результата, нельзя определить, соотносится ли с ним какой-то иной фактор.
К примеру, если в течение некоей последовательности дней, когда температура доходила до 80°F (примерно 26,6 °C), на углу улицы стояли две тележки с мороженым, трудно сказать о корреляции погоды и мороженщиков, поскольку нет вариации значения той или другой переменной (температуры или количества мороженщиков). То же справедливо и для случая, когда есть вариация только одной переменной – например, на улице всегда два мороженщика, а температура изменяется от 80 до 90 градусов. Этот сценарий показан на рис. 3.2: отсутствие вариации ведет к тому, что данные скопились в одной точке, а модуляция единственной переменной дает горизонтальную линию
[114]. Именно такой вариант в примере с грантом. Поскольку все результаты идентичны, нельзя сказать, что произойдет, если поменять шрифт или представить заявку за минуту до истечения срока.
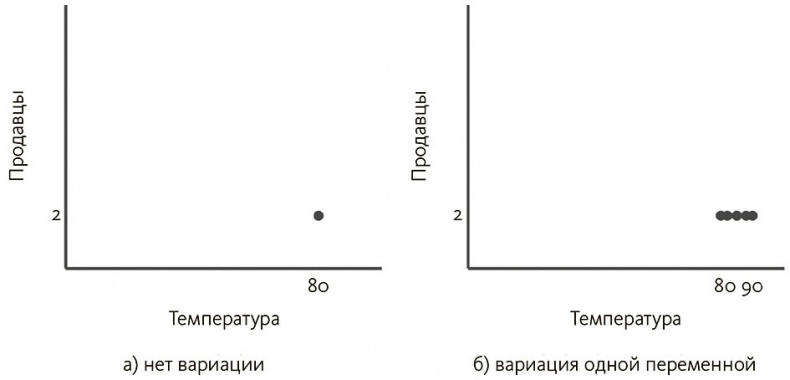
Рис. 3.2. Не наблюдая вариации обеих переменных, нельзя обнаружить корреляцию
И тем не менее широко распространена ситуация, когда анализируются только факторы, ведущие к определенному исходу. Только представьте, насколько часто победителей спрашивают, как именно они добились успеха, а потом стараются этот успех воспроизвести, выполняя в точности те же действия. Подобный подход полон недостатков по многим причинам, включая то, что люди просто не слишком хорошо умеют определять существенные факторы, недооценивают роль случайностей и переоценивают свои способности
[115]. В результате мы не только путаем факторы, которые по чистой случайности сопутствуют желаемому эффекту, с теми, которые действительно его обеспечивают, но и видим иллюзорные корреляции там, где их нет.
К примеру, многие интересуются, действительно ли музыкальное образование соотносится с профессиональными успехами в других областях. Даже если мы обнаружим, что многие успешные люди (как бы мы ни определяли успех) играют на музыкальных инструментах, эти ничего не скажет о существовании корреляции – не говоря уже о причинно-следственной связи. Если напрямую спросить, верят ли они, что музыка помогает развивать и другие способности, многие, безусловно, отметят некую взаимосвязь. Но с гораздо меньшей вероятностью они сделают это, если интересоваться конкретно умением играть в шахматы, быстро бегать или тем, сколько кофе вы выпиваете каждый день.
Для целей этой книги важнее всего следующее: беседы с победителями бесполезны, поскольку можно сделать то же самое, но не преуспеть. Возможно, все кандидаты оформляют заявки на грант шрифтом Times New Roman (а значит, те, кто не получил гранты, порекомендуют использовать другой шрифт), а может, успешные кандидаты получили грант, несмотря на избыточное количество иллюстраций в документах. Не зная совокупности положительных и отрицательных примеров, мы не сможем даже предположить наличие корреляции.
Корреляции: измерение и интерпретация
Скажем, мы исследуем студенческий пул, чтобы выяснить, сколько чашек кофе молодые люди выпивают перед финальным экзаменом, а потом регистрируем полученные баллы. Гипотетические данные этого примера представлены на рис. 3.3 (а). Корреляция очень сильна и равна почти 1 (0,963, если быть точными), поэтому точки на графике тесно окружают некую невидимую линию. Если взять обратное отношение (0 чашек кофе соответствуют 92 экзаменационным баллам, а 10 чашек – 10 баллам), чтобы сформировать отрицательную ассоциацию, абсолютное значение окажется тем же, а единственное, что изменится, – знак коэффициента корреляции. Тогда показатель измерения будет равен почти –1 (–0,963), а кривая станет отраженным по горизонтали вариантом положительно коррелирующих данных, как показано на рис. 3.3 (б).
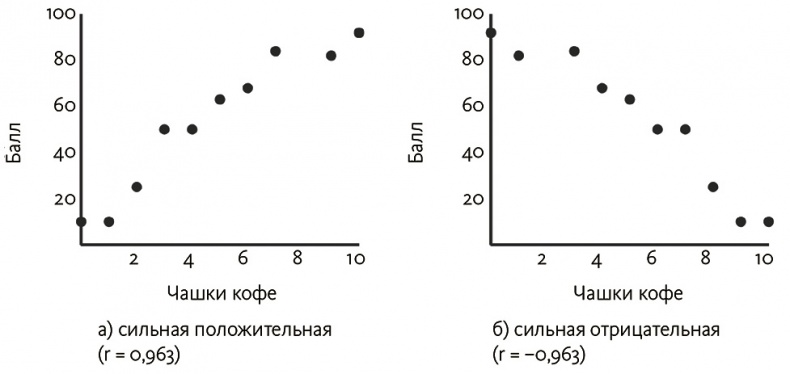
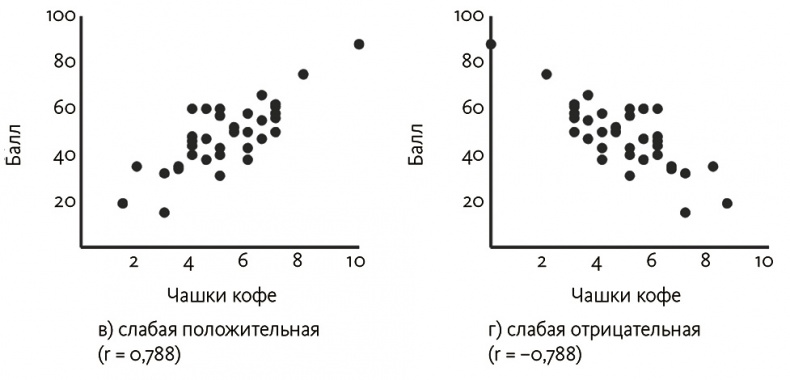
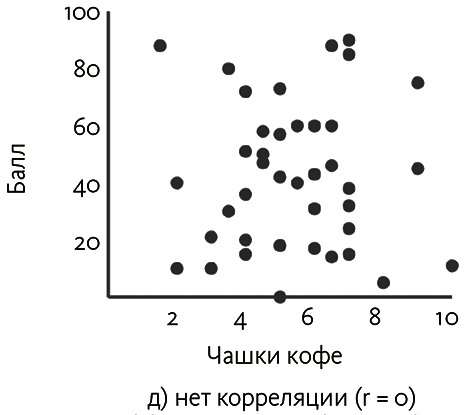
Рис. 3.3. Корреляции между потреблением кофе и экзаменационными баллами
С другой стороны, если бы каждое из этих отношений стало слабее и имела место повышенная вариация результатов экзамена для каждого уровня потребления кофе, наблюдалась бы дисперсия точек, и корреляция была бы слабее. Это продемонстрировано на рис. 3.3 (в), где точки на графике по-прежнему имеют в основном линейную форму, но отклоняются от центра гораздо дальше.
Как и ранее, инверсия отношения (потребление кофе коррелирует с худшими оценками) формирует кривую на рис. 3.3 (г), где единственным отличием оказывается нисходящий уклон.
Заметим, что, если отношение слабое, гораздо труднее перейти от значения потребления кофе до экзаменационных баллов и обратно. Это четко видно, если в первых примерах выбор значения одной из переменных сильно ограничивает вероятные значения другой. Но если мы попытаемся предсказать экзаменационные баллы для 4 чашек кофе с более слабой корреляцией, прогноз будет гораздо менее точен, поскольку мы наблюдали более широкий диапазон баллов для такого уровня потребления кофе. Предел для этой возрастающей вариации – пара переменных, которые абсолютно не соотносятся (имеют нулевой коэффициент корреляции), как показано на рис. 3.3 (д), при этом нельзя вообще ничего сказать о результатах экзаменов на основе выпитого кофе.






