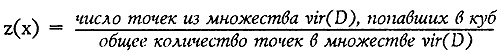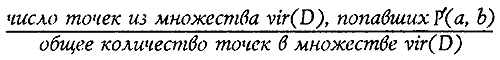Итак, задача состоит в том, чтобы выяснить, существует ли вообще такая естественная мера близости на множестве всех виртуальных династий, которая позволила бы уверенно отделить зависимые династии от независимых. То есть чтобы «расстояние» между заведомо зависимыми династиями было «мало», а «расстояние» между заведомо независимыми династиями было «велико». Причем требуется, чтобы эти «малые» и «большие» значения существенно отличались бы друг от друга, например, чтобы они были отделены одним или несколькими порядками.
Оказывается, такая мера близости, то есть «расстояние между династиями», действительно существует. К описанию такого коэффициента с(а, b) мы сейчас и перейдем.
Итак, мы построили в пространстве R15 некоторое множество династий D. Были смоделированы две наиболее типичные ошибки, делавшиеся летописцами. Каждая династия из множества D была подвергнута возмущениям типов (1) и (2). При этом каждая точка из D размножилась в несколько точек, что привело к увеличению множества. Получившееся множество мы обозначали через vir(D). Оказалось, что множество vir(D) состоит примерно из 15 × 1011 точек.
Будем считать «династический вектор а» случайным вектором в Rk, пробегающим множество vir(D). Тогда по множеству vir(D) мы можем построить функцию z плотности вероятностей. Для этого все пространство R15 было разбито на стандартные кубы достаточно малого размера так, чтобы ни одна точка из множества vir(D) не попала на границу какого-либо куба. Если x — внутренняя точка куба, то, положим:
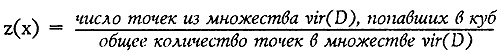
Ясно, что для точки x, лежащей на границе какого-либо куба, можно считать, что z(x) = 0. Функция z(x) достигает максимума в области, где сосредоточено особенно много династий из множества vir(D), и падает до нуля там, где точек из множества vir(D) нет, рис. 19. Тем самым график функции z(x) наглядно показывает, как именно распределено множество виртуальных династий vir(D) по пространству Rk. Другими словами, где это множество «густое», «плотное», а где оно разрежено.
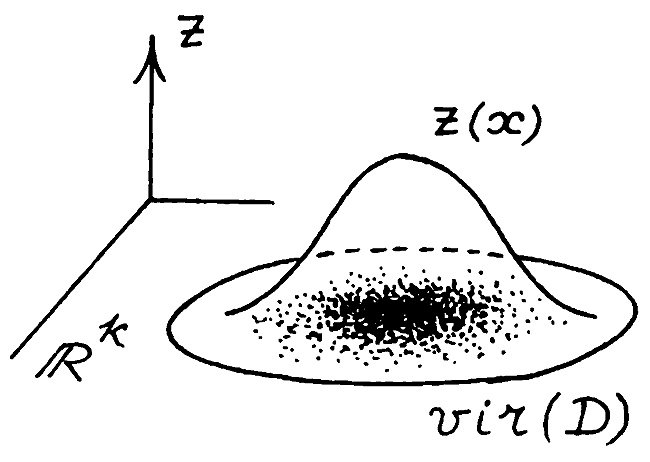
Рис. 19. Функция плотности, показывающая распределение точек множества vir(D).
Пусть теперь нам заданы две династии:
а = (a1, …, ak) и b = (b1, …, bk),
и мы хотим оценить, насколько они близки или далеки. Построим k-мерный параллелепипед P'(A, В) с центром в точке а, имеющий в качестве диагонали вектор а — b, рис. 20. Если спроектировать параллелепипед P'(a, b) на i-ю координатную ось, то получится отрезок с концами
[ai — |ai — bi|, ai + |ai — bi|].
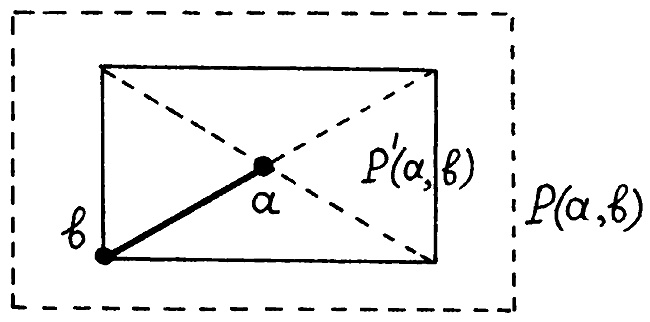
Рис. 20. Параллелепипеды Р'(а, b) и Р(а, b).
В качестве предварительного коэффициента с'(а, b) мы возьмем число:
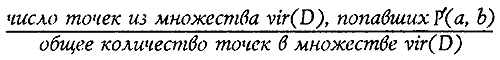
Ясно, что число с'(а, b) является интегралом функции плотности z(x) по параллелепипеду P'(а, b).
Смысл предварительного коэффициента с'(а, b) ясен. Династии, то есть векторы из vir(D), попавшие в параллелепипед P'(а, b), естественно назвать «похожими» на династии a и b. В самом деле, каждая из таких династий удалена от династии а не более, чем от династии а удалена династия b. Следовательно, в качестве меры близости двух династий а и b, мы берем долю династий, «похожих» на а и b в множестве всех династий vir(D).
Однако такой коэффициент с'(а, b) пока недостаточно хорош, поскольку он никак не учитывает то обстоятельство, что летописцы определяли длительность правлений царей с какой-то ошибкой, причем обычно тем большей, чем дольше длительность правления. Другими словами, нам нужно учесть ошибку летописцев (3), обсужденную выше.
Перейдем к моделированию ошибки (3). Пусть T — это длительность правления. Ясно, что длительность правления можно рассматривать как случайную величину, определенную на «множестве всех царей». Обозначим через g(T) число царей, правивших T лет. В работе [884] автор настоящей книги экспериментально вычислил эту гистограмму частот g(T) (плотность распределения указанной случайной величины) на основе данных, приведенных в хронологических таблицах Ж. Блера [76]. Положим h(T) = 1/g(T) и назовем h(T) функцией ошибок летописцев. Ошибка h(T) в определении длительности T тем больше, чем с меньшей вероятностью случайная величина — то есть длительность правления — принимает значение T. Другими словами, небольшие, «короткие» длительности правлений царей лучше поддаются вычислению летописцев. Здесь хронист ошибается незначительно. Напротив, большие длительности правлений царей, встречающиеся довольно редко, летописец обычно вычисляет с существенной ошибкой. Чем больше длительность правления, тем большую ошибку он может совершить.
Функция ошибок h(T) для указанной плотности вероятностей случайной величины (длительности правления) была определена экспериментально [884], с. 115. Разобьем отрезок [0,100] целочисленной оси T на десять отрезков одинаковой длины, а именно:
[0, 9], [10, 19], [20, 29], [30, 39], [90, 99].
Тогда оказывается, что
h(T) = 2, если T изменяется от 0 до 19,
h(T) = 3, если T изменяется от 20 до 29,
h(T) = 5([T/10] — 1), если T изменяется от 30 до 100.
Здесь через [s] обозначена целая часть числа s, рис. 21.
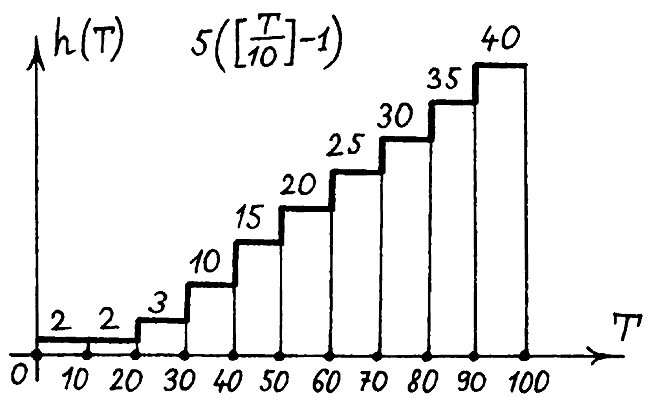
Рис. 21. Экспериментально вычисленная «функция ошибок летописцев».
Учтем теперь ошибки летописцев при построении «окрестности» точки а. Для этого расширим параллелепипед P'(а, b) до большего параллелепипеда P(а, b), центром которого по-прежнему является точка а, и ортогональными проекциями на координатные оси являются отрезки с концами
[ai — |ai — bi| — h(ai), аi + |аi — bi| + h(ai)].
Ясно, что параллелепипед P'(а, b) целиком лежит внутри большого параллелепипеда P(а, b), см. 20. Диагональю этого большого параллелепипеда является вектор а — b + h(а), где вектор h(а) выглядит так:
h(а) = (h(а1), …, h(ak)).
Его можно назвать ВЕКТОРОМ ОШИБОК ЛЕТОПИСЦЕВ.