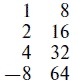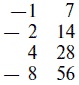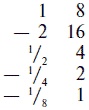Если, например, школьник желал вычислить произведение 8 на 8, эта трудная задача записывалась так:
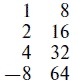
Очевидно, его познаний в устном счете хватало лишь для умножения на 2. Странно, но правильного метода деления чисел у него тоже не было, и похоже, что школьник вряд ли ясно представлял себе, что такое деление. Он спрашивал себя не о том, сколько раз 7 содержится в 77, а о том, на какое число надо умножить 7, чтобы произведение было равно 77. Чтобы получить ответ на свой вопрос, он писал таблицу умножения 7 на различные малые числа, а потом пытался определить, какие из этих произведений дают в сумме 77.
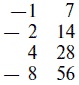
В этом примере множители, дающие в результате 7, 14 и 56, ученик отметил чертой, а эти числа вместе составляют нужное число. Таким образом, чтобы получить 77, необходимо умножить 7 на 1 + 2 + 8, то есть на 11. Если бы вопрос был «сколько раз 8 содержится в 19», иными словами, какое число нужно умножить на 8, чтобы получить 19, результат сложения:
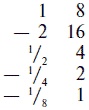
показывал, что нужными числами были 2, 1/4 и 1/8, поскольку парные им числа в сумме составляют как раз 19. Мы бы сказали: 8 содержится в 19 23/8 раза.
В связи с этим несовершенным пониманием деления легко понять, что египетский ученик не знал дробных чисел в том смысле, который это понятие имеет в нашей арифметике. Он вполне мог понять, что можно разделить вещь на несколько частей, и имел для такой части отдельное обозначение, например, ре-мет – «рот десяти», что означало «одна десятая». Но эта часть для него всегда была одна, он никогда не думал о ней во множественном числе. Египтяне могли сказать: «одна десятая и десятая и десятая» или «одна пятая и одна десятая», но привычное нам понятие 3/10 в уме египтянина не существовало. Но было одно исключение: для 2/3 у него были особые слово и знак, и это была у него единственная дробь не из разряда простейших. Когда он должен был делить меньшее число на большее, например 5 на 7, он не мог изобразить результат в виде дроби 5/7, как делаем мы, а был вынужден делать это крайне утомительным обходным путем. Он анализировал эту задачу, либо деля 1 на 7 пять раз, чтобы результат был 1/7 + 1/7 + 1/7 + 1/7 + 1/7, или делил два раза 2 на 7 и один раз 1 на 7, причем второй способ был более распространен. Существовали специальные таблицы, в которых египтянин мог найти практические результаты деления на 2 нечетных чисел первой сотни. Так он получал 1/4 1/28 1/4, 1/28, 1/7, которые он знал, как потом привести к виду 1/2 + 1/7 + 1/14.
Если с помощью такого громоздкого механизма египтяне получали точные результаты, то лишь благодаря тому, что работа была рутинная. Тематика примеров была так узка, что для каждого из них существовала установленная формула. Каждый расчет имел особое название и короткую общепринятую формулу, которую после того, как применил ее один раз, было легко повторять. Предлагаемый здесь пример вычисления может проиллюстрировать то, что было сказано только что.

Мне трудно представить себе, чтобы даже самый опытный математик смог бы догадаться, что означают эти цифры, и, лишь сравнивая похожие вычисления, мы можем понять все эти сокращения. Предположение, сформулированное в строке а, соответствует уравнению х + 1/5 = 21, результат которого х = 171/2 совершенно верно указан в строке д. Поскольку египтянин не очень хорошо умел выполнять вычисления с дробями, он на следующем шаге должен был вычислить эту несчастную 1/5 х. Это он делает так: в строке б умножает искомое число и пятую часть этого числа на 5, в сумме это дает 6. В строке в 21 делится по громоздкому египетскому способу на это 6, результат равен 31/2. Эти 31/2 были бы искомым числом, если бы раньше мы в строке б не превратили дробь 6/5 в число 6, умножив ее на 5; поэтому результат нашего деления должен быть в пять раз больше. Это умножение выполняется в строке г и дает в результате 171/2. В строке д результат проверен сложением этого 171/2 с 1/5, определенной раньше, то есть с числом 31/2, и в результате получается верная сумма – 21 из условия нашей задачи. В нашей современной записи все решение выглядело бы так:
а) 6/5 х = 21
б) 6 х = 21 х 5
в) х = 21/6 х 5
г) х = 31/2 х 5
д) х = 171/2
Проверка: 171/2 + 31/2= 21
О геометрии египтяне знали еще меньше, чем об арифметике, хотя им было крайне необходимо умение измерять площадь участка поверхности из-за того, что каждый год разлив уничтожал очень много границ между полями. Все их расчеты имели в основе прямоугольник, площадь которого они верно определяли как произведение длин двух его сторон. Но, как ни странно, они совершенно не замечали, что нельзя обращаться одинаково со всеми четырехсторонними фигурами, у которых противоположные стороны имеют одинаковую длину. И поскольку египтяне рассматривали каждый четырехугольник как четырехугольник, у которого две стороны совпадают одна с другой, а две остальные вдвое короче этих, они переносили эту ошибку и в вычислительные операции над треугольниками. Кроме того, для них равнобедренный треугольник был равен половине произведения длин его длинной и короткой сторон, потому что они во всех случаях определяли площадь соответствующего ему четырехугольника как произведение длин двух его сторон, словно это был просто прямой угол. Ошибка, возникавшая из-за заблуждений такого рода, в определенных обстоятельствах могла быть велика.
Вычисление площади трапеции тоже страдало от этой ошибки: чтобы определить ее площадь, они умножали длину наклонной стороны на половину произведения длин двух параллельных сторон. Как мы видим, основной принципиальной ошибкой данных египетских учеников в деле измерения площадей было то, что они так никогда и не поняли значение перпендикуляра. Вместо него они пользовались одной из наклонных сторон и этим с самого начала лишили себя возможности работать правильно. Стоит отметить, что при таких ошибках они все же нашли правильный способ приблизительного вычисления площади круга; в этом случае они вычитали из диаметра его девятую часть, а остаток умножали сам на себя. То есть, если диаметр круга был равен 9 родам (здесь род – длина измерительного жезла, английская единица измерения. – Пер.), площадь круга, по их расчетам, была 8 х 8 = 64 квадратных рода, и этот результат отличался от верного всего лишь примерно на 2/3 квадратных рода.
Среди задач на измерение объема, которые пытались решить египтяне, было, например, определение того, сколько зерна входит в амбар определенного размера. Судя по тому немногому, что мы в настоящее время можем более или менее ясно понять в этих задачах, основные концепции египтян в этом случае были верны, но условия задач слишком сложны, чтобы мы могли составить о них какое-то определенное мнение. Но если бы мы и понимали их, они, вероятно, мало изменили бы наше общее впечатление от математики древних египтян, и наше заключение по ее поводу таково: об их теоретическом знании этой науки сказать почти нечего, но их практические познания в ней очень хорошо удовлетворяли простые потребности повседневной жизни.