Самый простой пример — способ упрочнения древесно-стружечных плит (ДСП). Сейчас это основной материал, из которого изготовляют мебель. Получают древесно-стружечные плиты из древесной стружки, которую пропитывают специальным клеем, а потом спрессовывают. Выяснилось, что прочность плиты выше, если стружка расположена в общей массе не как попало, а вытянута в длину в одном направлении. Как этого добиться?
Запишем в вепольном виде исходную ситуацию: клей В1 создает связующее поле Пс, которое склеивает стружку В2.
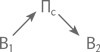
Прессование в этом технологическом процессе проводится над готовой массой, поэтому в схему конфликта его можно не включать. Необходимо вытянуть стружку в длину в одном направлении, причем желательно это сделать до заливки клеем — в густой массе двигать стружку будет значительно труднее.
Для этого на стружку нужно чем-то подействовать (слова, даже самые хорошие, не помогают!). Подействовать можно только полем, например, механическим — подуть на нее или раскрутить в центробежной машине. И если один конец стружки держать, то под действием этих сил стружка вытянется во всю длину. Но как поймать каждую за хвост? Вот если бы один конец был тяжелее другого...
Стружка — особа безответственная, неотзывчивая. Нет в ней внутренних свойств, за которые можно было бы «зацепиться». Поэтому схема прямого воздействия полем не срабатывает. Приходится вводить дополнительное вещество — В3.

Чтобы решить задачу, стружку предварительно обрабатывают мелким железным порошком, а потом помещают в магнитное поле. И каждая стружечка вытягивается «по ниточке» вдоль магнитной силовой линии. Теперь и клей можно вылить. Материал ДСП приобретает определенную структуру — структурируется.
Применение ферромагнитных частиц и магнитного поля в качестве руководящей и направляющей силы — один из наиболее известных, широко применяемых и перспективных методов. В технике для структурирования можно применять практически все известные поля: центробежные — при вращении более тяжелые элементы «отодвинутся» от оси вращения, вытянувшись по радиусу; акустические — за счет свойства колебаний создавать выступы и впадины, концентрировать энергию в местах образования «стоячих» волн при наложении колебаний; вызывать и использовать резонансные явления; тепловые — меняя температуру в различных точках, можно перемещать между этими точками вещества и объекты...
Проблема 2
ИЗМЕРЕНИЕ ДИАМЕТРА СКВАЖИНЫ
Чтобы выяснить, как действуют на верхний слой земли изменение температуры, влажность и др., в земле бурят скважины — круглые отверстия определенного диаметра — и измеряют этот диаметр при различных условиях. Чтобы повысить точность измерения, был создан специальный прибор в виде параллелограмма (рис. 13.2) — шарнирный четырехгранник. Две вершины параллелограмма А1 и А2 упираются в стенки скважины, а между двумя другими — В1 и В2 — с помощью пружины натянута струна. В зависимости от натяжения струны ее частота колебаний — звук — меняется.
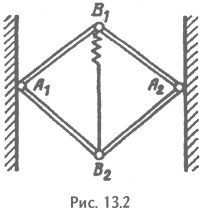
Это свойство и используется в приборе. Если диаметр скважины уменьшается, вершины А1 и А2 сближаются, а В1 и В2 расходятся, натягивая струну. Звук становится выше. И наоборот.
Как практически составлять вепольную формулу для решения задач такого типа, прекрасно описал Г.С. Альтшуллер на примере задачи об измерении с высокой точностью диаметра тончайшего провода. Задачу решали специалисты-изобретатели фантастического изобретательского бюро:
«На следующий день инженер из заводоуправления поехал в изобретательское бюро.
— Ясно, — сказали в бюро, выслушав инженера. — Задача простая. Пройдите в комнату 5, там сидит практикант, он вам поможет...
Практикант был совсем молоденьким. С сомнением поглядывая на практиканта, инженер изложил суть дела.
— Задачу мы решим легко, — сказал практикант. — Сначала запишем условия. Дано вещество, провод. Это вещество должно давать сигнал, сигнальное поле, несущее информацию о диаметре провода.
На листке бумаги он написал:
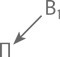
— Само по себе вещество такого поля не создает, — продолжал практикант. — Значит, надо приложить какое-то другое поле. Вот так:
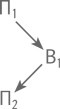
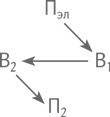
— Это вепольная схема изобретения, сделанного у вас на заводе, — пояснил практикант. — Ударим струну В1 (приложим к ней механическое поле П1), и возникнут колебания (механическое поле П2). Чтобы повысить точность, надо, во-первых, перейти от механических полей к электромагнитным; во-вторых, надо достроить веполь, введя второе вещество. Получится такая схема:
Электрическое поле действует на провод, заставляя его взаимодействовать со вторым веществом. А второе вещество посылает сигнал — какое-то поле П2, несущее информацию о диаметре провода. Вы какой бы сигнал предпочли?
— Световой, — сказал инженер. — Он удобнее.
— Значит, будем считать, что П2 — это оптическое поле. Итак, электромагнитное поле действует на провод, провод действует на какое-то вещество В2, а это вещество дает световой сигнал о диаметре провода. Задача решена: нужно только вспомнить физику девятого класса. Вот, взгляните...
Он протянул инженеру раскрытый учебник.
— Пожалуй, вы правы, — задумчиво произнес инженер, прочитав страничку. — Отличное решение! Странно, что мы сами не догадались!..
Нужно измерить диаметр микропровода. На тонких проводах легко возникает коронный разряд. Он зависит от диаметра провода. Как раз то, что нужно для решения задачи! По яркости и форме короны можно очень точно не только определить диаметр провода, но и проверить форму сечения: если провод овальный (а это плохо), корона тоже принимает овальную форму...»55
Описанные выше две задачи имеют одно общее свойство: это задачи на измерение. (Не забыли ли вы, кстати, что измерить — это значит сравнить с эталоном?) Иными словами, нам необходима информация об одном из параметров объекта. И получить ее прямым путем мы не можем — в этом особенность возникшей ситуации, причина появления задачи. Для ее решения приходится необходимую информацию преобразовать в другую форму, более удобную и доступную: поле на входе системы через промежуточное вещество создает поле на выходе.

