С учетом всего сказанного выше, мы можем заключить, что дополнения к китайскому кометному списку появились, скорее всего, лишь во второй половине XVIII — середине XIX века, Причем, сии были сделаны людьми, УЖЕ ЗНАВШИМИ О КОМЕТЕ ГАЛЛЕЯ И ПЫТАВШИМИСЯ ДОКАЗАТЬ, ЧТО КИТАЙЦЫ ЯКОБЫ НАБЛЮДАЛИ ЕЕ НА ПРОТЯЖЕНИИ НЕСКОЛЬКИХ ТЫСЯЧ ЛЕТ. Однако эти люди были плохими астрономами и подошли к делу слишком грубо и прямолинейно. Именно они, вероятно, и внесли в китайские кометные списки ПОДЛОЖНЫЕ наблюдения, образующие незамысловато-идеальную «китайской синусоиду» обращений кометы Галлея.
И последнее замечание. Если взять ВЕСЬ китайский список кометных наблюдений — а не только его часть, начиная с I века до н. э., как мы делали выше, — то 77-летний срок обращения кометы Галлея уже НИЧЕМ НЕ ВЫДЕЛЯЕТСЯ среди других значений, не имеющих к комете Галлея никакого отношения. Это значит, что взятые с потолка «времена обращения» кометы Галлея ровно с тем же успехом «подтверждаются» китайскими наблюдениями, как и истинное. А именно, для идеально полного представления ВСЕХ появлений кометы Галлея с 77-летним (истинным) сроком обращения в китайском кометном списке не хватает ДВУХ НАБЛЮДЕНИЙ. Но ТА ЖЕ САМАЯ картина наблюдается и для многих других ПРОИЗВОЛЬНО ВЫБРАННЫХ «времен обращения» кометы Галлея.
Таким образом, если мы расширим список китайских кометных записей, включив в него его древнейшую часть, никакого дополнительного подтверждения китайской хронологии по комете Галлея мы не получим. Наоборот, картина полностью размоется. Именно так и должно быть в случае НЕПРАВИЛЬНО ДАТИРОВАННЫХ НАБЛЮДЕНИЙ.
На рис. 31 мы приводим траекторию движения кометы Галлея по солнечной системе между двумя ее последовательными появлениями около Земли в 1836 и 1910 году.
На рис. 32 показана фотография кометы Галлея, сделанная в 1910 году, когда комета была очень хорошо видна в Северном полушарии.
5.7. О хаотической составляющей в движении кометы Галлея
В 1989 году в журнале «Astronomy and Astrophysics» появилась статья Б.В. Чирикова и В.В. Вячеславова [1066], в которой показано, что в движении кометы Галлея присутствует ЗНАЧИТЕЛЬНАЯ СЛУЧАЙНАЯ СОСТАВЛЯЮЩАЯ. На эту работу обратили наше внимание академик РАН, профессор МГУ д.ф.-м.н. В.В. Козлов и профессор МГУ д.ф.-м.н. А.И. Нейштадт.
Главный вывод своего исследования авторы сформулировали так: «Показано, что движение кометы Галлея ХАОТИЧНО БЛАГОДАРЯ ВОЗМУЩЕНИЯМ, ВЫЗЫВАЕМЫМ ЮПИТЕРОМ» [1066], с. 146.
Таким образом, движение кометы Галлея не является полностью детерминированным. Теория ее движения строится с помощью динамического хаоса. Причина в следующем. Если некоторая комета, как, например, комета Галлея, имеет сильно вытянутую орбиту, выходящую за круговую орбиту Юпитера, рис. 31, то каждый раз, возвращаясь назад в Солнечную систему, она встречает Юпитер в случайной фазе в силу несоизмеримости их времен обращения. Юпитер, как огромная планета, дает наибольший вклад в возмущение траектории кометы. Встречая его в случайной фазе, комета подвергается случайному возмущению.
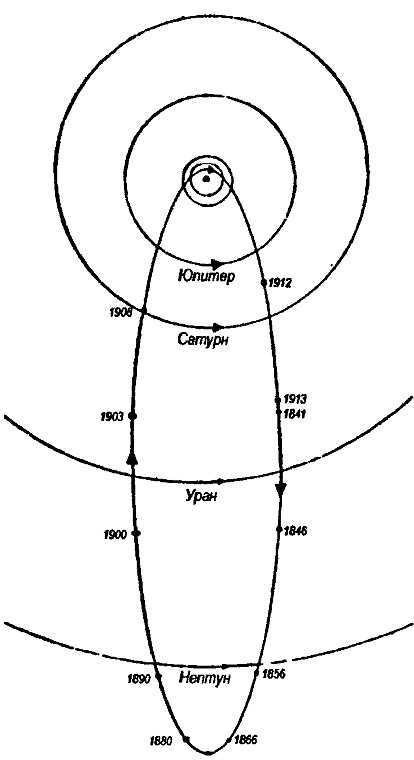
Рис. 31. Путь кометы кометы Галлея по солнечной системе между ее приходами в 1836 и 1910 годах. Взято из [544], т. 6, с. 140.
Оказывается, для комет, описываемых математической моделью, разработанной в статье [1066] — в том числе и для кометы Галлея — характерно наличие ХАОТИЧЕСКОЙ СОСТАВЛЯЮЩЕЙ В ИХ ДВИЖЕНИИ. Одним из наиболее чувствительных параметров кометной орбиты является время прохождения через перигелий. А следовательно — и ВРЕМЯ ОБРАЩЕНИЯ кометы, между двумя ее последовательными приближениями к Земле. В частности, время обращения кометы Галлея — СЛУЧАЙНАЯ ВЕЛИЧИНА с экспоненциально нарастающим разбросом.

Рис. 32. Комета Галлея в 1910 году. Взято из [544], т. 6, с. 141.
Но при наличии случайной составляющей, та идеальная «китайская синусоида» во временах обращения кометы Галлея, которую обнаружили Коуэлл и Кроммелин, НИКАК НЕ МОГЛА ОБРАЗОВАТЬСЯ.
5.8. Подозрительно высокая частота маловероятных событий в скалигеровской истории
Нам скажут: хотя и редко, но чудеса все-таки происходят. Может быть и на этот раз именно случай нарисовал нам идеальную китайскую синусоиду? Почему вы не хотите поверить, что она возникла просто случайно?
Конечно, случайно может возникнуть все — ответим мы. Например, обезьяна, случайно тыкая в клавиши пишущей машинки, может напечатать, — причем без ошибок — целый роман. Но вероятность такого события ничтожно мала, хотя и не равна нулю. Это значит, что прежде чем напечатать роман, наша воображаемая обезьяна в течении многих тысяч лет будет печать полную чепуху. Потом время от времени начнут появляться маленькие рассказы и обрывки разных романов. И, наконец, еще через много-много миллионов лет наступит, наконец, момент, когда из-под ее лапок действительно полезет роман целиком Причем — напечатанный совершенно случайно.
Вероятность появления «китайской синусоиды» в ДОСТАТОЧНО ДЛИННОМ ряду случайных испытаний тоже совсем ненулевая. Но, чтобы она проявила себя, испытаний должно быть действительно МНОГО. Грубо говоря, число испытаний по порядку величины должно сравняться с единицей, деленной на вероятность события. Появление же «китайской» синусоиды, по сути дела, В ОДНОЙ — ЕДИНСТВЕННОЙ СЕРИИ ИСПЫТАНИЙ настолько исчезающе мала, что ею можно смело пренебречь. Точно так же, как и вероятностью того, что какая-нибудь обезьянка, сев за пишущую машинку, тут же лихо напечатает нам без пропусков и ошибок четыре тома романа «Война и Мир».
Причем, это касается не только «китайской синусоиды» но и маловероятных событий в истории вообще. Как в свое время Н.А. Морозову, так и нам нередко приходится сталкиваться с глубоким непониманием природы маловероятных событий. И почему-то это непонимание особенно сильно начинает проявляться, как только речь заходит об ИСТОРИИ. Как один из ярких примеров, процитируем слова МАТЕМАТИКА Б.А. Розенфельда, опубликовавшего статью «Математика в трудах Н.А. Морозова» [583], с. 129–138. Комментируя обнаруженные Н.А. Морозовым поразительные и МНОГОЧИСЛЕННЫЕ совпадения в традиционной истории, Б.А. Розенфельд писал:
«Морозов подсчитывал вероятность тех или иных совпадений, и, найдя что эта вероятность чрезвычайно мала, делал вывод о невозможности этих совпадений. Такого рода рассуждения СОВЕРШЕННО НЕПРАВОМЕРНЫ (? — Авт.), так как теория вероятностей является наукой о массовых, а не о единичных явлениях, и ФАКТИЧЕСКИ МОГУТ ПРОИСХОДИТЬ СОБЫТИЯ, ВЕРОЯТНОСТЬ КОТОРЫХ СКОЛЬ УГОДНО БЛИЗКА К НУЛЮ» [583], с. 137.
Причем, Б.А. Розенфельд формально совершенно прав в своем последнем высказывании. События со сколь угодно малой вероятностью действительно могут происходить. Но, как мы уже объяснили выше, если вы хотите, чтобы некое маловероятное событие действительно произошло, нужно совершить большое количество испытаний. В каждом из которых нужное вам событие может произойти с некоторой ненулевой вероятностью. При этом, количество испытаний должно быть порядка величины, обратной значению вероятности события в одном испытании. Итак, чем меньше вероятность события, тем больше испытаний нужно совершить, чтобы оно действительно произошло. Другими словами, важна не столько вероятность события сама по себе, сколько СООТНОШЕНИЕ ЭТОЙ ВЕРОЯТНОСТИ И КОЛИЧЕСТВО ИСПЫТАНИЙ, В КОТОРЫХ СОБЫТИЕ МОЖЕТ ПРОИЗОЙТИ.

