Можно также задаться вопросом, в какой степени способность к пространственным манипуляциям влияет на легкость, с которой люди пользуются своими образами при решении задач. Во второй главе я ссылался на эксперименты со сканированием мысленных образов, сформированных с помощью визуальных изображений или вербальных описаний. В этих экспериментах было показано, что время, необходимое для мысленного сканирования расстояния между двумя объектами воображаемой сцены, прямо пропорционально реальному расстоянию между этими объектами. Предполагается, что мысленные образы являются достаточно точной репрезентацией, сохраняющей метрическую структуру трехмерного евклидова пространства.
Дэнис и Кокьюд (Denis and Cocude, 1997) предлагали 32 испытуемым сканировать образ вымышленного острова, сформированный на основе короткого рассказа c описанием относительного расположения нескольких ориентиров. Среди этих испытуемых были выделены те, кто получил высшие и низшие баллы по Миннесотскому бланковому тесту: соответственно, по 12 человек с высоким и низким уровнем развития зрительно-пространственных образов. Первые сканировали значительно быстрее, чем вторые, но эти группы различались также по степени взаимосвязи между расстоянием и временем сканирования. У группы людей с высокой образностью эта взаимосвязь была четко выраженной и статистически значимой (r = 0.84), а у людей с низкой образностью – слабой и статистически незначимой (r = 0.32). Из этих результатов следует, что испытуемые с относительно высокой пространственной способностью с большей легкостью формируют и анализируют ментальные репрезентации, содержащие метрическую информацию о множестве физических объектов.
Манипулирование мысленными образами
Результаты экспериментов с мысленным сканированием, которые были описаны выше, показывают, что пространственные отношения между объектами в структуре образа соответствуют отношениям между этими объектами в физическом пространстве. Далее необходимо выяснить, соответствуют ли способы манипуляции представленными объектами тем способам, посредством которых можно манипулировать реальными физическими объектами.
Как отмечалось выше, некоторые тесты на пространственную способность включают процесс мысленного вращения, который был детально изучен Шепардом и Метцлер (Shepard and Metzler,1971). Они предъявляли испытуемым выполненные на компьютере рисунки с различными перспективными планами объемных объектов, сконструированных путем соединения 10 одинаковых кубиков (см. рис. 3.1). Предъявляли пары рисунков, изображавшие: а) один и тот же объект, видимый в разных ориентациях в двухмерном пространстве; б) один и тот же объект, видимый в разных перспективах в трехмерном пространстве; в) объект и его зеркальное отображение.
Шепард и Метцлер обнаружили, что время, необходимое для сравнения различных ракурсов одного и того же объекта, прямо пропорционально углу между этими ракурсами (угол изменялся от 0 до 180 градусов), и что нет существенной разницы между объектами, расположенными в плоскости рисунка, и объектами, развернутыми в глубину. Отсюда следует, что испытуемые мысленно поворачивали трехмерные репрезентации одного или обоих объектов с постоянной скоростью до тех пор, пока объекты не занимали сходную ориентацию в пространстве (когда становилось уже наглядно видно, одинаковые эти объекты или разные). Все испытуемые утверждали, что использовали образы для выполнения этого мысленного вращения.
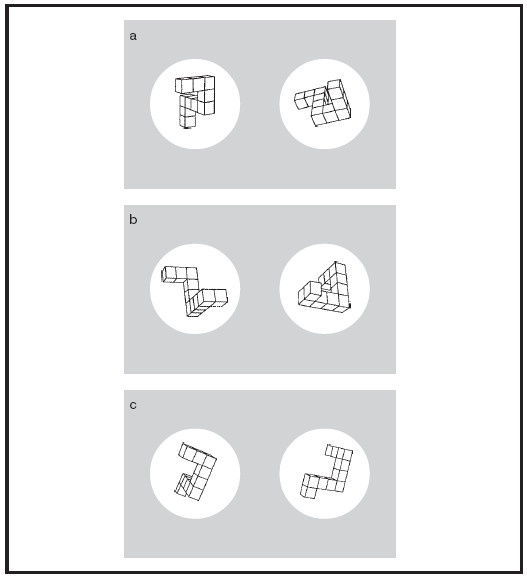
Рис. 3.1. Примеры пар перспективных объемных рисунков, предъявляемых испытуемым:
a – пара идентичных объектов, один из которых повернут относительно другого на 80 градусов в плоскости рисунка; b– пара идентичных объектов, один из которых повернут относительно другого на 80 градусов в глубину; c – пара различных объектов, совпадения которых нельзя добиться при любом повороте. (Shepard and Metzler, 1971)
Возникает вопрос, будут ли испытуемые действовать аналогичным образом, если им надо выполнить целую последовательность таких манипуляций. Шепард и Фенг (Shepard and Feng, 1972) искали ответ на этот вопрос в экспериментах с предъявлением изображений, состоящих из шести соединенных между собой квадратов, представляющих собой развертку граней бумажного куба на плоской поверхности. Испытуемым предлагали определить, встретятся ли две стрелки, нарисованные на краях разных квадратов, если эти квадраты опять собрать в куб. На рис. 3.2 показано несколько подобных задач; на каждом изображении темный квадрат обозначает фиксированное основание куба. В половине случаев стимулы относились к категории «совпадение», то есть две стрелки должны были встретиться (как в случае «a»); другая половина относилась к категории «несовпадение», то есть стрелки не могли встретиться (как в случае «b»). Идея этого эксперимента также основана на заданиях из тестов на пространственную способность.
И в этом эксперименте все испытуемые снова сообщали, что для выполнения задания они использовали образы: «Некоторые испытуемые описывали свои образные переживания как преимущественно зрительные; другие говорили о сильном кинестетическом компоненте, добавлявшемся при представлении того, как они собирают куб своими руками» (Shepard and Feng, 1972, р. 242). Первичный анализ результатов показал, что время ответа для случая «совпадение» зависело от количества сгибов, которые необходимо сделать для совмещения стрелок при выполнении этого задания на реальном кубе. Например, фигура «c» на рис. 3.2. требует пяти отдельных сгибов и выполнение этого задания занимает больше времени. Шепард и Фенг утверждали, что даже в простейшем случае «d», когда стрелки уже встретились, тем не менее нужно сделать один сгиб, чтобы расположить квадраты под углом 90 градусов.
Тщательный анализ данных выявил, однако, что время ответа в большей степени зависит от общего числа квадратов, включенных в выполнение каждого сгиба. Действительно, испытуемые отвечали медленнее, даже если дополнительные квадраты не имели прямого отношения к соединению стрелок, а просто придавали структуре «лишний вес» (как в случае «e» на рис. 3.2.). Шепард и Фенг предположили, что этот факт свидетельствует против гипотезы о том, что испытуемые выполняли задание с помощью каких-то вербальных умозаключений, поскольку это должно было привести к игнорированию избыточной информации. Наконец, время ответов уменьшалось, если стрелки стояли на противоположных концах прямой полосы из четырех квадратов, которую можно было «свернуть» одним движением, не делая четырех отдельных сгибов (как в случае «f»).
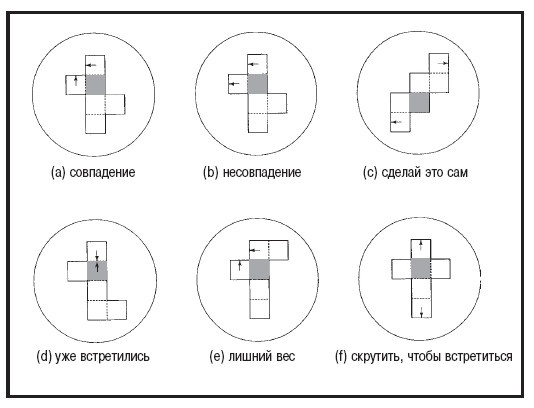
Рис. 3.2. «Сгибание в уме»: шесть иллюстративных задач. (Shepard and Feng, 1972)
Купер и Шепард (Cooper and Shepard, 1973) разработали более сложное задание, в котором испытуемые должны были решить, предъявлено ли им обычное изображение буквы или цифры или их зеркальное отображение. В каждой пробе испытуемого просили создать мысленный образ определенного символа в одном из шести возможных ракурсов; затем предъявляли символ, который находился в том же или в одном из других пяти ракурсов. Было показано, что время реакции увеличивается с увеличением разницы между предполагаемым и реальным ракурсом символа. На основании этих результатов Купер и Шепард сделали вывод, что испытуемые вращали свои зрительные образы с постоянной скоростью до тех пор, пока они не оказывались в том же ракурсе, что и тестовый символ. Эта гипотеза нашла свое подтверждение и в самоотчетах испытуемых о том, как образы помогали им в решении предъявленных задач.

