ЭКСТРАСЕНСОРНАЯ МАТЕМАТИКА
Попросите добровольца в аудитории загадать любое число, состоящее из одной-двух цифр. Затем скажите, что никоим образом не можете знать, что это за число, и предложите сделать следующее.
1. Удвойте число.
2. Прибавьте 12.
3. Разделите сумму на 2.
4. Вычтите из нее исходное число.
Спросите: «Думаете ли вы сейчас о цифре 6?» Опробуйте этот трюк сначала на себе и увидите, что данная последовательность вычислений всегда в итоге приводит к цифре 6, какое бы число вы изначально ни выбрали.
Почему это работает
Этот трюк целиком основан на простой алгебре. Я иногда использую его как способ познакомить с алгеброй студентов.
Секретное число, выбранное добровольцем, можно обозначить как х. Тогда выполняемые действия представляем так:
1. 2х (удвоить число).
2. 2х + 12 (прибавить 12).
3. (2х + 12)/2 = х + 6 (разделить на 2).
4. х + 6 — х (вычесть исходное число).
Не важно, какое число выбрано, итоговый ответ всегда будет 6. При повторении данного приема попросите добровольца прибавить другое число на втором шаге (скажем, 18). Итоговый ответ будет половиной этого числа (а именно 9).
МАГИЯ ЧИСЛА 1089
Следующий трюк существует уже не одно столетие. Сделайте так, чтобы человек из аудитории достал ручку и бумагу:
1) и тайно записал трехзначное число, цифры которого идут в порядке уменьшения (например, 851 или 973);
2) записал число в обратном порядке и вычел его из исходного числа;
3) к полученному ответу добавил его же, только в обратном порядке.
В конце последовательности магическим образом появится ответ 1089, какое бы число ни выбрал доброволец. Например:
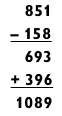
Почему это работает
Независимо от того, какое трехзначное число вы или кто-либо другой выберете в этой игре, окончательный ответ всегда будет равен 1089. Почему? Обозначим аbс неизвестное трехзначное число. Алгебраически это эквивалентно:
100a + 10b + c.
Запись числа в обратном порядке (для вычитания из исходного) дает сbа, которое алгебраически равно:
100c + 10b + a.
После вычитания сbа из аbс выходит:
100a + 10b + c — (100c + 10b + a) = 100(a — c) + (c — a) = 99(a — c).
Поэтому после вычитания на шаге 2 должно получиться одно из следующих чисел, кратных 99: 297, 396, 495, 594, 693, 792 или 891. Каждое из них после прибавления к нему своей перевернутой версии в итоге даст 1089, что мы и видим на шаге 3.
ТРЮК С ПРОПУЩЕННОЙ ЦИФРОЙ
Используя число 1089 из предыдущего примера, вручите добровольцу калькулятор и попросите умножить 1089 на любое трехзначное число, не называя его. (Предположим, он тайно умножил 1089 х 256 = 278 784) Теперь поинтересуйтесь, сколько цифр в полученном ответе. Ответ — 6.
Затем попросите: «Громко назовите пять из этих шести цифр в любом порядке. Я попытаюсь определить недостающую». Предположим, доброволец громко перечисляет: «Два… четыре… семь… восемь… восемь». Вы вежливо говорите ему, что он пропустил цифру 7. Секрет основан на том, что число кратно 9 тогда, и только тогда, когда сумма составляющих его цифр кратна 9. Так как 1 + 0 + 8 + 9 = 18 кратно 9, значит, число 1089 кратно 9. Поэтому 1089 при умножении на любое целое число даст кратное 9. И раз уж прозвучавшие цифры в сумме дают 29, и следующее кратное 9, большее 29, это 36, то наш доброволец пропустил число 7 (так как 29 + 7 = 36).
Есть более утонченные способы заставить добровольца в конечном итоге прийти к кратному 9. Вот некоторые из моих любимых.
1. Пусть он наугад выберет шестизначное число, перемешает его цифры, затем отнимет меньшее из шестизначных чисел из большего. Поскольку мы производим вычитание двух чисел с одинаковой модульной суммой (в самом деле, сумма цифр идентична), полученная в итоге разность будет иметь нулевую модульную сумму, следовательно, число будет кратно 9. Далее продолжайте действовать, как было описано выше, чтобы найти недостающую цифру.
2. Пусть он тайно выберет любое четырехзначное число, запишет его в обратном порядке, а потом вычтет меньшее число из большего. (Получится кратное 9.) Затем пусть умножит результат на 3. Далее, как и раньше, вы ищете пропущенную цифру.
3. Попросите добровольца перемножать разные цифры до тех пор, пока их произведение не превратится в семизначное число. Это не гарантия получения числа, кратного 9, но на практике такую «гарантию» можно получить не меньше чем в 90 % случаев (с большой вероятностью перемножаемые цифры будут включать девятки или две тройки, или две шестерки, или 3 и 6). Я часто использую данный способ, выступая перед математически продвинутой публикой, которая может раскусить другие методы.
Однако существует одна проблема, за которой нужно постоянно следить. Предположим, прозвучавшие числа в сумме дают кратное 9 (скажем, 18). После такого ответа у вас не будет возможности определить, пропущен ли 0 или 9. Как справиться с этой ситуацией? Очень просто! Сжульничайте! Просто спросите: «Вы ведь не пропустили 0, не так ли?» Если 0 пропущен, то вы успешно провернули свой трюк. Если нет, скажите: «Ой, просто показалось, что вы отвлеклись! Вы не пропустили один, два, три или четыре, не так ли?» Доброволец либо покачает головой, либо скажет «нет». Затем вы продолжаете: «Как и не пропустили пять, шесть, семь или восемь. Вы не включили девять, не так ли?» Доброволец ответит утвердительно, а вы получите заслуженные аплодисменты!
СЛОЖЕНИЕ ЧЕХАРДА
Этот прием сочетает в себе быстрые вычисления в уме и поразительные предсказания. Вручите зрителю карту с расчерченными на ней десятью линиями, пронумерованными от 1 до 10.
Пусть он загадает два положительных числа от 1 до 20 и подпишет ими линии 1 и 2. Далее попросите его записать сумму 1-й и 2-й линий на линии 3. Затем сумму линии 2 и 3 на линии 4 и так далее, как проиллюстрировано ниже.

Пусть зритель покажет вам карту. Вы сразу же можете назвать ему сумму всех чисел на ней. Например, в нашем случае вы могли бы мгновенно объявить, что числа в сумме дают 671 (быстрее, чем зритель подсчитал бы это с калькулятором).