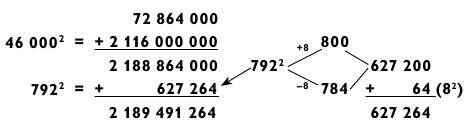
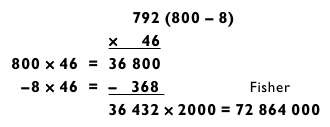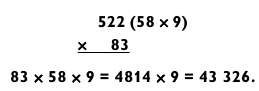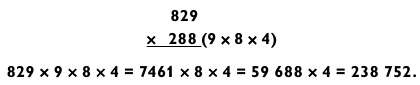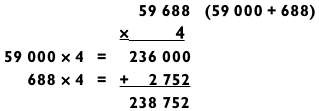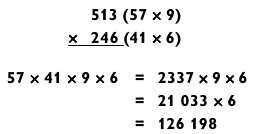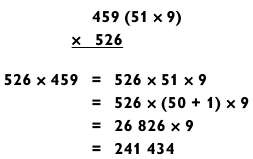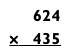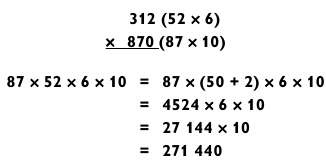Я сознаю, что процесс вычисления квадрата 46 7922 довольно громоздкий. Представляю вам схему того, как я возводил это число в квадрат:
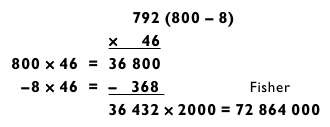
Рассмотрим другой пример на возведение пятизначного числа в квадрат: 83 5222.
Как и прежде, вычисляем ответ в таком порядке:
83 х 522 х 2000, 832 х 1 миллион, затем 5222.
В первой задаче обратите внимание на то, что 522 имеет делитель 9. Значит, 522 = 58 х 9. Раскладывая 83 как 80 + 3, получим:
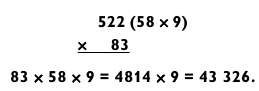
Результатом удвоения 43 326 будет число 86 652, что можно запомнить как 86 Julian. Поскольку 832 = 6889, мы можем произнести: «Шесть миллиардов…»
Сложение 889 + 86 = 975. Прежде чем произнести «975 миллионов», мы проверяем, не приведет сумма Julian (652 000) и квадрата 5222 к переносу единицы в разряд миллиардов.
Приблизительно оценив 5222 как 270 000 (500 х 540), убеждаемся, что переноса не будет. Поэтому можно спокойно сказать: «…975 миллионов…».
Наконец, возведение в квадрат 522 обычным способом приведет к числу 272 484, а его сложение с числом Julian (652 000) даст последнюю часть ответа: «…924 484».
В виде схемы решение данной задачи выглядит следующим образом:

УПРАЖНЕНИЕ: ВОЗВЕДЕНИЕ В КВАДРАТ ПЯТИЗНАЧНЫХ ЧИСЕЛ
1. 45 7952 2. 21 2312 3. 58 3242
4. 62 4572 5. 89 8542 6. 76 9342
УМНОЖЕНИЕ «3 НА 3»
Задачи на умножение типа «3 на 3» будут последним барьером на пути к грандиозному финалу в виде умножения «5 на 5».
Здесь, как и в случае с задачами типа «3 на 2», существует многообразие методов, которые могут быть использованы для упрощения процесса умножения.
Метод разложения
Начнем с метода разложения. К несчастью, большинство трехзначных чисел не раскладывается на множители в виде отдельных цифр, но если разложение найдется, процесс вычисления будет не таким уж и сложным.
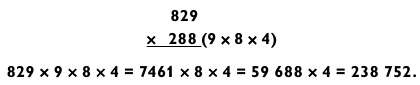
Обратите внимание на последовательность действий. Путем разложения 288 на 9 х 8 х 4 мы упрощаем задачу «3 на 3» (829 х 288) до «3 на 1 на 1 на 1». Далее она превращается в «4 на 1 на 1» (7461 х 8 х 4) и, наконец, в «5 на 1» для получения итогового ответа 238 752. Прелесть данного решения состоит в отсутствии каких-либо действий на сложение и в том, что ничего не нужно хранить в уме. Добравшись до задачи типа «5 на 1», мы оказались в одном шаге от окончательного ответа.
Задачу типа «5 на 1» можно решить в два действия, если представить 59 688 как 59 000 + 688, а затем сложить результаты задач «2 на 1» (59 000 х 4) и «3 на 1» (688 х 4), как показано ниже.
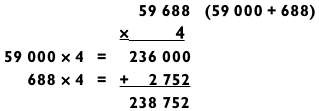
Если оба трехзначных числа можно разложить на «2 на 1», то задача «3 на 3» упрощается до «2 на 2 на 1 на 1», как в следующем примере.
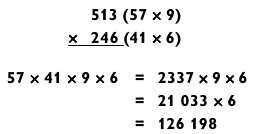
Как обычно, лучше сразу избавиться от трудного элемента задачи, то есть от умножения типа «2 на 2». Как только вы это сделаете, задача будет сведена к «4 на 1», а затем к «5 на 1».
Очень часто бывает так, что раскладывается только один из сомножителей. В таком случае задача сводится к умножению типа «3 на 2 на 1», как в этом примере:
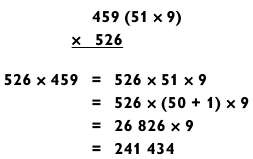
Следующая задача «3 на 3» в действительности просто замаскированная задача типа «3 на 2».
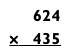
Путем удвоения 435 и уменьшения 624 наполовину получаем эквивалентную задачу.
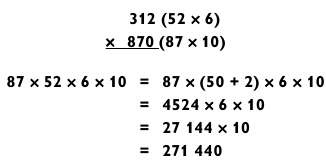
Метод совместной близости
Вы готовы к чему-нибудь попроще? Следующий прием, который был представлен еще в главе 0, основан на такой алгебраической формуле:
(z + a)(z + b) = z
2 + za + zb + ab
Переписываем ее:
(z + a)(z + b) = z(z + a + b) + ab
Эта формула справедлива при любых значениях z, a и b.
Мы будем пользоваться ею всякий раз, когда трехзначные числа, которые нужно перемножить (z х a и z х b), находятся близко к легкому числу z (типичный случай, когда число z имеет большое количество нулей). Например, умножим