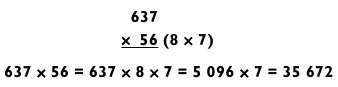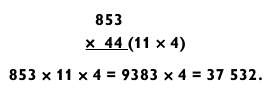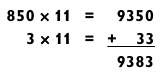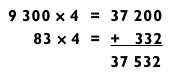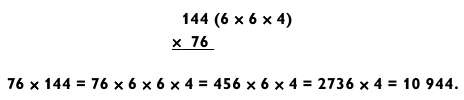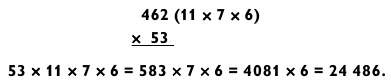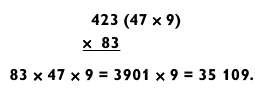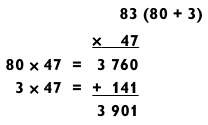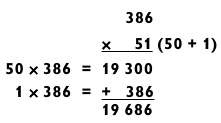Далее прибавляем квадрат числа 247. Не забудьте, что 247 можно быстро получить как дополнение для 753. Затем переходим к окончательному ответу, как это сделано в предыдущем примере.
УПРАЖНЕНИЕ: КВАДРАТЫ ЧЕТЫРЕХЗНАЧНЫХ ЧИСЕЛ
1. 12342 2. 86392 3. 53122
4. 98632 5. 36182 6. 29712
УМНОЖЕНИЕ «3 НА 2»
В ходе решения задач типа «2 на 2» мы уже убедились в существовании нескольких путей решения одного и того же примера. Многообразие методов увеличивается параллельно росту количества цифр в задаче. В случае задач «3 на 2» я предпочитаю «предварительный просмотр» для определения самого оптимального метода расчета.
Методы разложения
Самые легкие задачи типа «3 на 2» — те, в которых двузначные числа можно разложить на сомножители. Например:
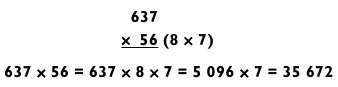
Потрясающе, что здесь не нужно ничего складывать. Вы просто представляете 56 как 8 х 7, затем решаете пример на умножение типа «3 на 1» (637 х 8 = 5096) и, наконец, пример типа «4 на 1» (5096 х 7 = 35 672). Больше не требуется никаких дополнительных действий, и необходимости запоминать промежуточные результаты тоже нет.
Свыше половины всех двузначных чисел раскладываются на сомножители, среди которых число 11 и меньшие числа. Поэтому данный метод подойдет для многих задач. Вот пример:
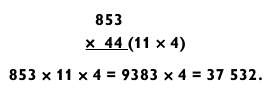
Чтобы умножить 853 х 11, представьте 853 в виде 850 + 3 и далее рассуждайте так:
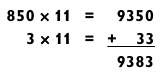
Теперь умножим 9383 х 4, представив 9383 как 9300 + 83, следующим образом:
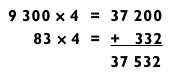
Если двузначное число не раскладывается на сомножители (или они большие), рассмотрите возможность разложения трехзначного числа.
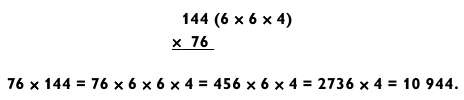
Обратите внимание, что последовательность умножений выстроилась из задач типа «2 на 1», «3 на 1» и, наконец, «4 на 1».
Это те задачи, которые вы уже умеете решать с легкостью. Поэтому тип примеров «3 на 2» не должен оказаться сложным для вас.
Еще один пример, где не двузначное число подвергается разложению, а трехзначное.
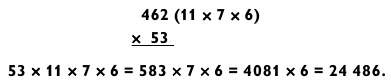
Здесь последовательность задач типа «2 на 2», «3 на 1» и «4 на 1». Но если трехзначное число имеет множитель 11, можно использовать метод умножения на 11 (как описано в главе 4) и получить простой пример типа «2 на 2» (53 х 11 = 583). В данном случае нахождение сомножителя 11 у числа 462 оправдывает себя.
Если двузначное число не раскладывается на «хорошие» сомножители, а трехзначное раскладывается только на сомножители в виде «2 на 1», с задачей все еще можно легко справиться путем умножения типа «2 на 2», а затем «4 на 1», как показано в следующем примере:
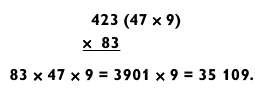
Здесь необходимо учесть, что 423 делится на 9 и исходная задача преобразуется в 83 х 47 х 9. В данном случае пример «2 на 2» не настолько прост, но если представить 83 в виде 80 + 3, получится следующее:
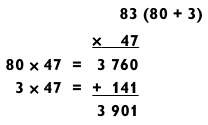
Теперь решаем задачу типа «4 на 1» в виде 3901 х 9 для получения итогового ответа 35 109.
Метод сложения
Когда двух- и трехзначное числа в задаче типа «3 на 2» не поддаются простому разложению, можно прибегнуть к методу сложения.

Данный метод предполагает суммирование ответов задач на умножение типа «2 на 2» и «2 на 1». Такого рода задачи включают в себя более сложные элементы (нежели те, которые имеют место в методе разложения), поскольку при решении примера «2 на 1» приходится держать в уме пятизначное число, а затем складывать результаты. Возможно, проще решить эту задачу путем разложения 721 на 103 х 7 и последующего вычисления 37 х 103 х 7 = 3811 х 7 = 26 677.
Вот другой пример:

Хотя обычно при использовании метода сложения на слагаемые разбивается трехзначное число, порой разбиение двузначного числа более удобно, в особенности если его последние цифры равны 1 или 2, как в следующем примере.
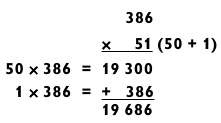
Это превращает задачу «3 на 2» в «3 на 1», делая ее абсолютно легкой, так как второе действие представляет собой умножение на 1. Заметьте, кстати, 5 здесь умножается на четное число, что дает дополнительный 0 в ответе. Поэтому в задаче на сложение надо суммировать только две цифры.
Другой пример умножения 5 на четное число показан в следующей задаче: