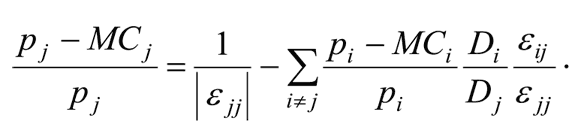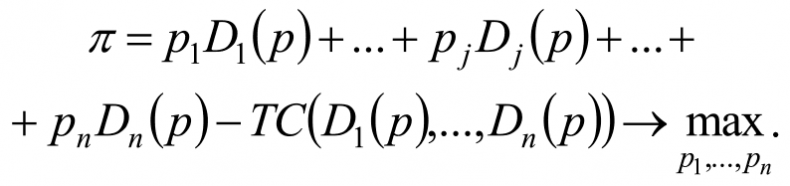
Для решения задачи нужно приравнять к нулю все частные производные функции прибыли по ценам и решить соответствующую систему из n уравнений. Заметим, что цены на товары выбираются независимо друг от друга (то есть ∂pi / ∂pj = 0 при i≠j), а спрос взаимосвязан, поэтому частные производные выручки от продажи i-го товара по j-й цене, рассчитываемые как производные произведения, примут следующий вид:
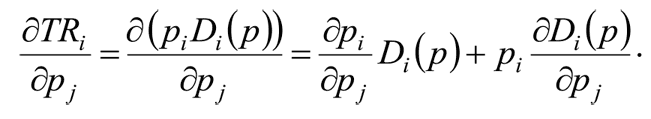
Каждая такая выручка вносит свой вклад в прибыль, равно как изменение цены pj влияет на спрос, а значит, и на выпуск всех товаров, что в свою очередь дает соответствующую добавку к издержкам. Таким образом, итоговая производная прибыли компании по j-й цене равна
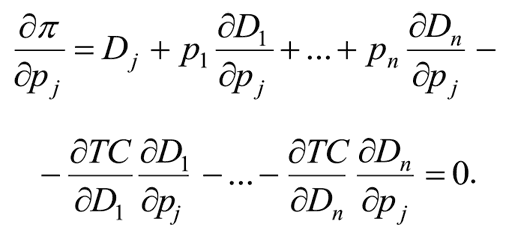
Рассмотрим теперь некоторые частные случаи. И первым из них будет случай независимого спроса и независимых издержек. Это означает, что, во-первых, спрос на i-й товар зависит исключительно от собственной цены и никак не связан с ценами других товаров: ∂Di / ∂pj = 0, а во-вторых, издержки описываются так называемой «сепарабельной функцией»
TC(D1(p), …, Dn(p)) = TC1(D1(p)) + … + TCn(Dn(p)).
В этой ситуации задача многопродуктовой монополии распадается на множество задач определения оптимальных цен на отдельные товары и ничем не отличается от случая, рассмотренного в предыдущем параграфе:
Dj + pj Dj' – TCj' Dj' = 0.
Здесь и далее мы будем обозначать как Dj' производную спроса на j-й товар по собственной цене, а TCj' – предельные издержки производства j-го товара.
Небольшие различия в постановках можно найти во второй ситуации – ситуации независимого спроса и связанных издержек. Функция издержек уже не является сепарабельной, и изменение выпуска j-го товара может, например, за счет задействования общих производственных мощностей, трудовых ресурсов либо технологий повлиять на затраты на производство остальных товаров. Это означает, что производная функции прибыли по j-й цене примет вид
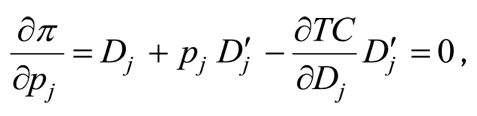
и оптимальная цена будет удовлетворять следующему уравнению:
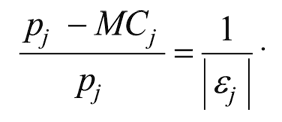
Заметим, что формула совпадает с ее аналогом для однопродуктовой монополии, но с одним отличием: предельные издержки MCj связаны с изменением суммарных издержек по всем товарам при изменении выпуска j-го.
Можно рассмотреть аналог этой модели с немного другой интерпретацией. Двухпериодная вариация под названием «Learning by doing» заключается в том, что издержки производства со временем сокращаются за счет обучения, и чем больше продукции мы произведем в первом периоде, тем ниже будут издержки во втором, то есть ∂TC2 /∂q1 < 0.
Действительно, фирма, только входящая на рынок и обеспечивающая небольшой спрос, еще не знает всех тонкостей бизнес-процессов, не выявила лучших контрагентов, ее предельные издержки достаточно велики, а значит, и в будущем это может сказываться на прибылях не лучшим образом. Но если уже в первый период выпуск нарастает, то фирме выгодно даже ценой некоторых затрат находить наилучшие каналы сбыта и поставки сырья, принимать на работу лучших работников и вкладываться в повышение их квалификации, что положительно влияет на эффективность в будущем.
Данный принцип «сегодня учимся, а в результате завтра производим дешевле» и является основополагающим в модели. При этом будущие прибыли учитываются не номинально, а с некоторым дисконтирующим множителем, меньшим единицы. Задача монополиста принимает следующий вид:
π = p1 D1(p1) + δ p2 × D2(p2) – TC1(D1(p1)) – δ TC2(D2(p2), D1(p1)) → max.
Приравняв к нулю частные производные по каждой из цен, получим, что во втором периоде будет установлена монопольная цена (третьего периода не существует – «после нас хоть потоп», и монополист действует классическим образом). А в первом периоде цена оказывается ниже монопольной для сокращения будущих издержек.
5.1.3. Многопродуктовая монополия: связанный спрос
В предыдущем параграфе изучалась ситуация независимого спроса, однако часто производитель выпускает или продает множество связанных товаров, являющихся субститутами или комплементами. Например, если производитель выводит на рынок йогурт с новым вкусом, это, конечно, может привлечь новых покупателей, но может также сказаться на продажах уже зарекомендовавших себя видов продукции. В частности, не следует забывать про «эффект каннибализации», когда компания, выпускающая новые продукты, фактически конкурирует сама с собой и отъедает у себя старые сегменты рынка.
Напротив, компания, предоставляющая дополнительные услуги (доставку, страховку, расширенные программы сервиса), может тем самым увеличить спрос на основной продукт. Равно как и снижение цены основного продукта привлекает к нему больше покупателей, а значит, фирма может компенсировать выпадающие доходы за счет продажи дополнительных услуг.
Решение задачи максимизации прибыли в этой ситуации принимает следующий вид.