При С = 0 получаем функцию оптимальной ставки f (v) = v (n – 1) /n. То есть если число участников аукциона в приведенной задаче увеличивается с двух до пяти, то ставка игрока с оценкой 600 тысяч рублей поднимется с 300 до 480, в случае десяти участников – до 540, а в случае 100 участников – до 594 тысяч рублей.
Второе обобщение более серьезное – мы откажемся от нереалистичного предположения о равномерном распределении ценностей на отрезке и рассмотрим произвольный случай. Итак, пусть распределение ценностей участников аукциона задано функцией F(v). Данная функция показывает вероятность того, что ценность объекта не превышает сумму v. Для того чтобы победить на аукционе, нужно, чтобы ставки всех участников не превосходили нашу, а ценности для всех участников, исходя из симметричности равновесия и монотонности f (v), были не больше, чем для нас. Таким образом, вероятность победы будет равна G (f –1(b)) ≡ F n–1 (f –1(b)), а максимизируемая функция ожидаемого выигрыша примет вид (v – b) G (f –1(b)). Продифференцируем ее по ставке b, снова принимая в расчет, что v = f –1(b):
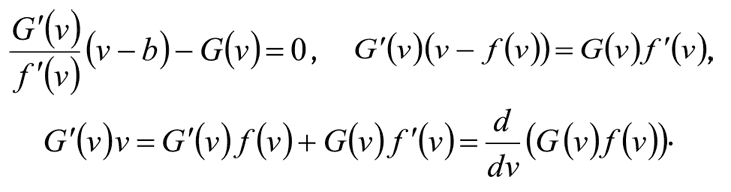
Решив полученное дифференциальное уравнение, найдем равновесную функцию ставки для общего случая аукциона первой цены:
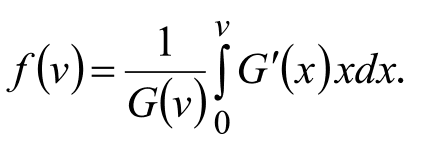
Заметим, что из нее легко получить результаты для рассмотренных выше частных случаев. Например, в случае равномерного распределения ценностей получим следующие результаты.
Для двух участников: G(v) = v,
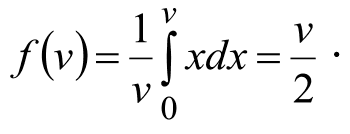
Для произвольного n: G(v) = v n–1,
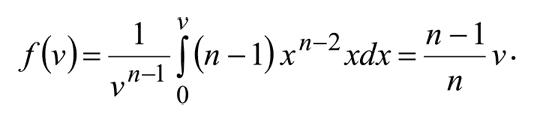
Еще два общих вывода можно получить, если с помощью интегрирования по частям записать равновесную функцию ставки в еще одном виде:
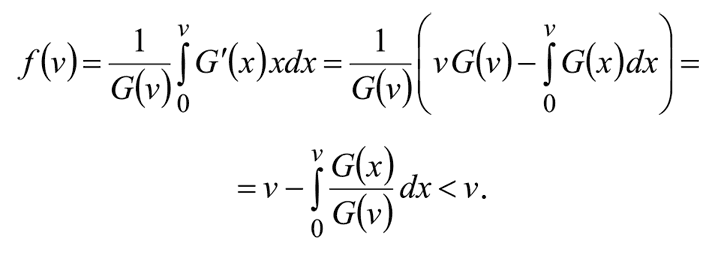
Напрямую из выведенной формулы видно, что при любом распределении ценностей оптимальная ставка будет строго ниже оценки объекта. Это первый важный вывод, теперь доказанный строго.
Перейдем теперь в этой формуле от функции G(v) обратно к F(v):
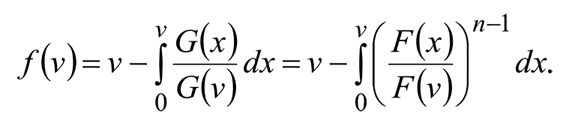
Из нее следует второй важный вывод для аукциона первой цены, который выполняется вне зависимости от распределения ценностей: чем больше участников аукциона, тем ближе к оценке объекта должна быть ставка.
3.2. Теорема об эквивалентности форматов
3.2.1. Постановка теоремы Майерсона
В предыдущем разделе книги мы рассмотрели два варианта закрытых аукционов и вывели оптимальные стратегии для их участников. Но остался открытым вопрос о том, какой из этих форматов выгоднее использовать, если целью аукциониста является максимизация доходов, полученных от продажи лота. И не стоит ли придумать какой-то еще более изощренный механизм (например, аукцион третьей или четвертой цены), чтобы прибыль организаторов стала еще выше.
В 1981 году Роджер Майерсон доказал удивительный результат, названный теоремой об эквивалентности форматов. Он продемонстрировал, что средний выигрыш аукциониста, продающего объект на аукционе первой цены, в точности совпадет со средним выигрышем на аукционе Викри. Более того, как ни трудно в это поверить, средний выигрыш продавца в закрытых аукционах вообще не зависит от правил их проведения, если выполняются три очень простых свойства: объект отдается участнику, который подал максимальную заявку; участник с нулевой оценкой ничего не платит; равновесие симметрично.
Именно эта теорема в 2007 году принесла Майерсону Нобелевскую премию по экономике. И неслучайно. Это действительно мощнейший механизм анализа аукционов и конструирования их дизайна.
Разберем его более подробно.
Предположим, что аукцион организован некоторым образом – пока совершенно произвольно, но именно в виде статической, а не динамической игры. Это означает, что участники в конвертах или в электронной системе однократно подают заявки и существует единое для всех правило, определяющее выплаты, а также участника, который объявляется победителем аукциона, или нескольких участников, между которыми объект продажи разыгрывается в лотерею с заданными вероятностями.
Возьмем для определенности первого участника. Задать формат аукциона – означает задать отображение
сопоставляющее каждому размеру заявки b1 ∈ R первого участника и каждому неупорядоченному набору заявок {b2,…, bn} ∈ B остальных участников платеж m1 = m (b1; {b2,…, bn}) первого участника в таких условиях. Это означает, что аукцион определяется суммой денег, которую должен будет заплатить участник в зависимости от собственной ставки и ставок всех его конкурентов.
Для формулировки и доказательства теоремы об эквивалентности форматов нам потребуется в дополнение к симметричности правила, которое определяет выплаты, ввести три дополнительных требования.
Как говорилось ранее, первым из них является эффективность. Объект, выставленный на продажу, всегда достается участнику с максимальной ставкой. Формально говоря, теорему можно трактовать шире, и вместо эффективности требовать одинаковой функции размещения объекта. Это может быть актуально в случае делимых благ. Например, если на аукционе разыгрывается пакет акций, то можно отдать 80 % акций победителю, а оставшиеся 20 % – указавшему вторую ставку. Но тогда и сравнивать этот аукцион придется исключительно с другими аукционами с такой же функцией размещения 80 на 20. Поэтому, чтобы не усложнять задачу, пока будем рассматривать предположение об эффективности в классическом виде.

