Возьмём небольшую выборку из десяти школьников, у которых следующие значения массы тела:
42, 43, 43, 42, 45, 46, 40, 41, 41, 42.
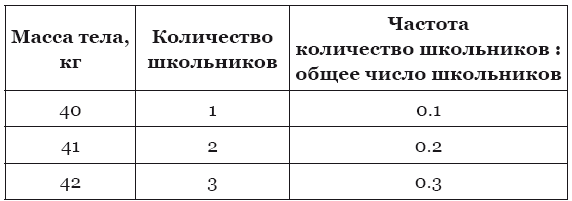
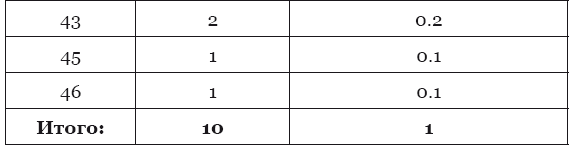
Теперь мы можем построить график по нашей таблице. По горизонтальной оси отложим массу тела, а по вертикальной – частоту встречаемости той или иной массы тела.
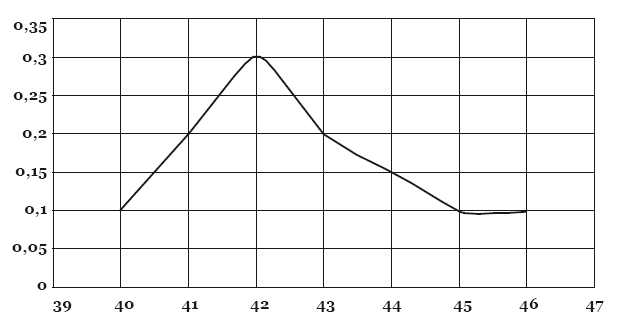
С помощью определённых статистических тестов (как правило, никто, кроме студентов, не делает это вручную, все считают на компьютере) можно определить, насколько получившаяся картина близка к виду нормального распределения. Чем больше точек поставлено на график, тем он, соответственно, будет точнее.
Если результат статистического теста говорит о том, что распределение близко к нормальному, мы должны применять группу статистических тестов, названных параметрическими. Если же распределение отличается от нормального, следует применять непараметрические методы.
Параметрические методы
Что же это за параметры, на которых будет базироваться обработка наших данных? Нашу выборку мы можем описать определённым образом, используя для этого ряд характеристик. Самое простое, что проходят даже в школе, – это среднее. Из нашей выборки 42, 43, 43, 42, 45, 46, 40, 41, 41, 42 мы можем легко найти среднее, просто сложив все числа и поделив их на количество элементов в выборке: 42+43+43+42+45+46+40+41+41+42 = 425, 425: 10 = 42.5. Чуть сложнее находится среднеквардратическое отклонение и ряд других параметров. Параметрические методы названы параметрическими, так как они основываются на оценке полученного распределения.
Однако иногда среднее может нам ничего не сказать. Самая простая ситуация – средняя температура по больнице. Если выборка будет достаточно большой, то средняя температура в любом отделении больницы может оказаться в норме, но это вовсе не будет говорить о том, что пациенты здоровы. Однако температура человека находится в строго определённых пределах и, безусловно, будет подчиняться закону нормального распределения. Что же мы тогда сможем узнать, найдя среднюю температуру в больнице? Мы только опишем наше распределение: температура человека, как правило, будет близка к 37 °C.
Среднеквадратическое отклонение (СКО) в статистике показывает, насколько широк разброс в нашей выборке. Например, для нашей выборки оно будет равно примерно 1.75. Как правило, СКО записывается через знак ±. Тогда мы получаем, что нашу выборку можно описать как минимум так: 42.50±1.75. Это означает, что большая часть элементов выборки находится в пределах от 42.50-1.75 = 40.75 до 42.50+1.75=44.25. В данном случае мы записываем именно 42.50, а не 42.5, так как этого требуют правила математической записи: в СКО у нас получилось 2 знака после запятой.
Среднее и СКО не всегда хорошо описывают выборку, об этом надо помнить. Если распределение асимметрично, данные будут искажены. Для описания таких выборок есть медиана. Если вновь провести аналогию с геометрией, как мы делали ранее для доказательств, то медиана – это отрезок, соединяющий вершину треугольника с серединой противоположной стороны (рис. 6).
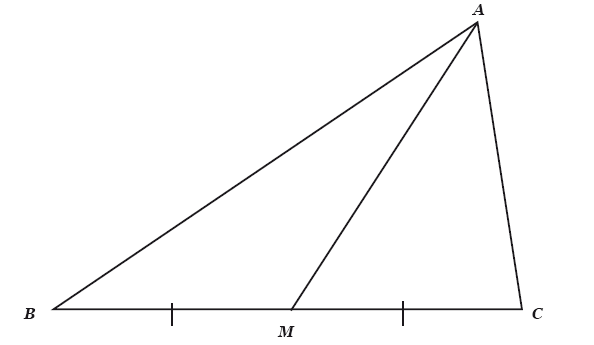
Рис. 6. В треугольнике ABC отрезок AM является медианой, то есть разделяет сторону BC пополам
Аналогичную функцию медиана выполняет в статистике применительно к распределению величин. Медиана в статистике – это такое значение, которое разделяет распределение пополам, то есть половина значений распределения больше медианы, а половина – меньше (рис. 7). Мода – ещё один статистический параметр, обозначающий значение, которое встречается наиболее часто в нашей выборке.
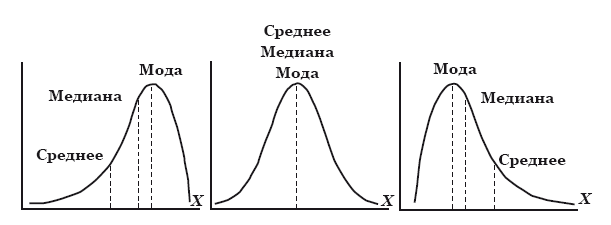
Рис. 7. Среднее, медиана и мода. Слева направо: ассимметричное распределение, нормальное распределение и ассимметричное распределение
Как видно из рис. 7, для идеального нормального распределения среднее и медиана должны совпасть (как и в случае с равнобедренным треугольником), однако если нам нужна информация о том, какое именно значение находится в середине асимметричного распределения, медиана будет гораздо предпочтительнее. Кроме медианы, существуют так называемые процентили, наиболее часто из них используются квартили, то есть 25-й и 75-й процентили. Эти показатели показывают четверть наибольших и наименьших показателей в распределении. Сама медиана считается 50-м процентилем (рис. 8).
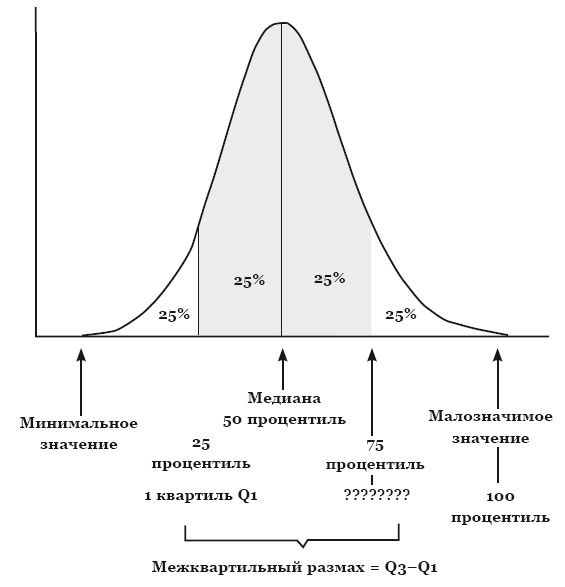
Рис. 8. Распределение с обозначенными минимальным и максимальным значениями, а также медианой и 25-м и 75-м процентилями
Итак, получается, что если наше распределение имеет вид идеальной гауссианы, мы легко можем оперировать параметрами распределения, но если распределение отличается от нормального, нам начинает не хватать среднего и СКО, необходимо вводить другие характеристики, такие как процентили и медиана.
Так как эти статистические характеристики наиболее понятны и просты, параметрические методы в статистике получили большую популярность. Практически ни одно исследование не обходится без их применения. Возраст, масса тела, рост, некоторые биохимические показатели – эти характеристики вполне соответствуют нормальному распределению, а значит, данные можно обрабатывать параметрикой. К параметрическим методам относятся, например, t-критерий Стьюдента, знакомый многим студентам, например по выполнению лабораторных по физике.
Критерий Стьюдента. Самый любимый и самый понятный! По сути он является частным случаем более сложного метода анализа, однако при изучении статистики рациональнее всегда начинать с изучения именно критерия Стьюдента. Данный метод позволяет нам сравнить, насколько отличаются две выборки друг от друга. В англоязычной литературе чаще называется просто t test (подозреваю, что это из-за сходства в написании Student [Стьюдент] и student [студент], что значительно усложняет поиск в Интернете).

