Сейчас в городах живет более 50 процентов мирового населения. Та добавка к экспоненциальному росту, которую дает коэффициент масштабирования Уэста, вполне может быть ключевым элементом привлекательности городов. По-видимому, когда большое количество людей оказывается вместе, получаемые результаты становятся больше, чем изначальные вложения. Вероятно, поэтому люди и переезжают в большие города. Когда человек перебирается в город вдвое большего размера, он внезапно начинает получать на 15 процентов больше – во всех областях.
Тот же закон масштабирования затрагивает и инфраструктуру, но в обратном направлении. Оказывается, при удвоении размера города не требуется вдвое больше материалов: действует экономия на инфраструктуре. Стоимость медного провода, асфальта, канализационных труб на душу населения уменьшается на 15 процентов. Это означает, что вопреки распространенному мнению и ваш личный «углеродный след» оказывается тем меньше, чем крупнее город, в котором вы живете.
К сожалению, этот математический принцип определяет масштабирование не только положительных аспектов. Преступность, заболеваемость и плотность дорожного движения возрастают с тем же коэффициентом. Если, к примеру, вам известен уровень заболеваемости СПИДом в городе с 5-миллионным населением, то для оценки этого же показателя для города, в котором живут 10 миллионов человек, первую цифру нужно не просто удвоить, а еще и добавить к результату 15 процентов. Все те же волшебные 15 процентов.
Есть ли объяснение такому универсальному масштабированию самых разных городов? Существует ли что-то вроде ньютоновского закона всемирного тяготения, применимого ко всему на свете – от яблок до планет и черных дыр?
Чтобы понять, почему город определяется не физическими размерами, а численностью населения, важнее всего осознать, что город состоит не из зданий и улиц, а из людей, которые в нем живут. Город – это сцена, на которой разыгрывается история цивилизации, и разыгрывают ее не актеры, а акторы. Города ценны постольку, поскольку они выполняют функцию сетей, обеспечивающих возможность взаимодействия между людьми.
Значит, модель города должна отражать не его географическое положение, будь то на острове или посреди пустыни, а сетевую структуру взаимодействий его жителей. По-видимому, свойство универсальной масштабируемости, открытое Уэстом, определяется именно качеством сети, возникающей из взаимодействий горожан. Таково могущество математики. Она позволяет увидеть простые структуры, находящиеся в самом сердце нашей сложной среды.
Если взять предельный случай – когда по мере роста города каждый житель контактирует со всеми остальными, – можно увидеть, почему крупный город порождает сверхлинейный рост. Если численность его населения равна N, максимальным числом связей между ними будет количество разных рукопожатий, которые могут совершить эти N жителей. Выстроим их в ряд и пронумеруем от 1 до N. Горожанин номер 1 проходит вдоль ряда, пожимая всем руки, – всего N – 1 рукопожатий. После него вдоль ряда проходит горожанин номер 2. Он уже пожал руку горожанину № 1, так что он прибавляет к сумме N – 2 рукопожатий. Так продолжается и дальше, и на долю каждого следующего горожанина приходится на одно рукопожатие меньше. Общее число рукопожатий равно сумме чисел от 1 до N – 1. Давно не виделись! Это то самое вычисление, которое задали Гауссу. Его шорткат дал формулу для вычисления этого числа:
Что происходит с количеством связей при удвоении N? Число рукопожатий не удваивается, а увеличивается в 2 в квадрате – то есть 4 – раза. Число рукопожатий пропорционально квадрату числа жителей города.
Этот пример прекрасно показывает, почему математика может избавить нас от необходимости снова и снова изобретать колесо. Хотя я задал совершенно другой вопрос, касавшийся связей в сети, оказалось, что для анализа роста этого числа у меня уже есть инструменты, полученные из анализа треугольных чисел. Действующие лица могут то и дело меняться, но сценарий остается тем же. Стоит понять этот сценарий, и в вашем распоряжении оказывается шорткат к пониманию поведения любых персонажей пьесы. В данном случае число связей между горожанами растет с увеличением их количества квадратично.
Разумеется, каждый житель города никак не может быть знаком со всеми остальными. Более консервативной гипотезой будет предположение о том, что горожане знакомы с жителями своего района. Но эта величина масштабируется линейно; общие размеры не имеют существенного значения.
Судя по всему, связи между жителями городов находятся где-то между этими двумя предельными случаями. Горожанин поддерживает все свои местные связи плюс несколько более дальних связей в других частях города. По-видимому, именно такие дальние связи и приводят к тому, что при удвоении численности населения количество связей увеличивается на лишние 15 процентов. Как я объясню в последующих разделах этой книги, сети такого типа возникают во многих разных сценариях, и это обстоятельство оказывается чрезвычайно удобным для прокладки шорткатов.
Паттерны обманчивые
Хотя паттерны обладают невероятной силой, использовать их следует с осторожностью. Вы можете отправиться по такому пути, считая, что, вероятно, знаете, куда вы идете. Но иногда этот путь может завернуть в странном и неожиданном направлении. Возьмем ту последовательность, которую я предлагал вам решить раньше:
Что, если я скажу вам, что следующее число в этой последовательности – не 32, а 31?
Если взять круг, отмечать на его окружности точки и соединять все эти точки прямыми линиями, каково будет максимальное число областей, на которые можно разделить этот круг? Если точка всего одна, никаких линий не будет и область получится тоже всего одна. Если добавить еще одну точку, две точки можно соединить линией, которая разделит круг на две области. Добавим третью точку. Проведя все возможные линии, соединяющие эти точки, получим треугольную фигуру, окруженную тремя секторами круга: всего четыре области.

Рис. 1.1. Первые пять чисел деления круга
Если продолжить действовать таким же образом, кажется, что проявляется паттерн. Вот данные по числу областей, получающихся при добавлении очередных точек на окружности:
В этот момент разумно предположить, что добавление очередной точки удваивает число областей. Проблема заключается в том, что этот паттерн нарушается, как только я добавляю шестую точку. Как ни старайся, число областей, на которые линии разбивают круг, оказывается равным 31. А вовсе не 32!
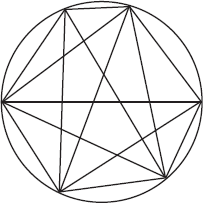
Рис. 1.2. Шестое число деления круга

