Биологические компьютеры
А как насчет задачи коммивояжера? Можно ли найти шорткат к ней при помощи нетрадиционных средств? Одну из задач, родственных задаче коммивояжера, исследователям удалось решить, применив компьютер очень необычного типа. В этой задаче – так называемой задаче о гамильтоновом пути – нужно проложить маршрут по сети дорог с односторонним движением, соединяющих нанесенные на карту города́.
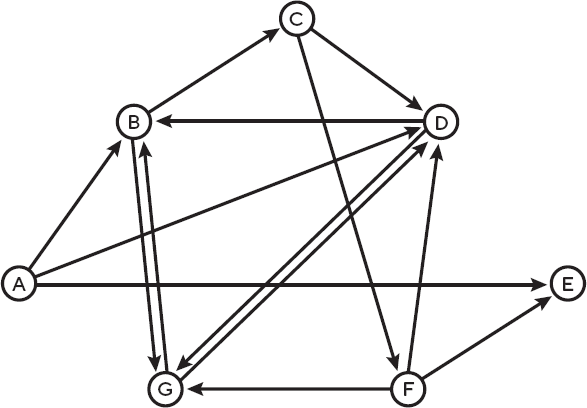
Рис. 10.4. Задача о гамильтоновом пути: как попасть из города А в город E, посетив все остальные города только по одному разу?
Требуется найти маршрут, начинающийся из одного города, скажем А, и заканчивающийся в другом городе – Е, – нопроходящий через все остальные города по одному, и только одному, разу. Возможен ли такой маршрут? Оказывается, найти его так же трудно, как решить задачу коммивояжера. Но и эта задача прекрасно подходит для применения параллельной обработки информации. Однако математик Леонард Адлеман не стал обращаться к квантовому миру, а придумал интересный биологический подход к ее решению. К слову, именно фамилию Адлемана обозначает буква А в аббревиатуре RSA, названии шифровальной системы, использующей простые числа для обеспечения безопасности сетевых транзакций.
В 1994 году Адлеман объявил на семинаре в MIT об изобретении суперкомпьютера, который он построил для решения задачи о гамильтоновом пути. Он назвал его TT-100, но его слушатели очень удивились, когда он достал из кармана пиджака обычную пробирку. Буквы ТТ означали test tube
[132], а число 100 – объем этой пластмассовой пробирки, 100 миллилитров. Роль микропроцессоров, работавших в пробирке, играли небольшие нити ДНК.
Нити ДНК составляются из четырех оснований, которые обозначают буквами A, T, C и G
[133]. Эти основания стремятся попарно соединяться друг с другом: А с Т, а C – с G. Если получить короткие одиночные нити, составленные из этих оснований, – так называемые олигонуклеотиды, – каждая из них попытается найти другую нить, основания которой могут образовывать пары с ее собственными. Например, нить АСА попытается найти нить TGT, с которой она может соединиться и образовать устойчивую двойную нить ДНК.
Идея Адлемана состояла в следующем: присвоим каждому городу на карте, по которой мы пытаемся проложить маршрут, метку, представляющую собой нить из 8 оснований. Затем, если между двумя городами есть односторонняя дорога, создадим нить ДНК с 16 основаниями, первые 8 из которых содержатся в метке города отправления, а вторые 8 – это основания, дополнительные к содержащимся в метке города, в который ведет дорога. Если есть дорога, ведущая в город А, и дорога, ведущая из него, две нити этих дорог, содержащие по 16 оснований, соединятся: последние 8 оснований дороги, ведущей в город А, свяжутся с первыми 8 основаниями дороги, ведущей из него.
Любой маршрут проезда по этим городам по таким дорогам может быть воспроизведен в нитях ДНК, соединяющихся во всех случаях, когда одна дорога входит в город, а другая выходит из него.
Например, у города А может быть метка ATGTACCA, у города B – GGTCCACG, а у города C – TCGACCGG. Тогда дороге из А в B будет соответствовать нить
а дороге из B в C – нить
Восемь последних оснований первой из этих дорог могут соединиться с восемью первыми основаниями второй, что показывает, что маршрут, позволяющий попасть из города А в город C, существует.
Эта система прекрасна тем, что такие нити ДНК можно приобретать в больших количествах в коммерческих лабораториях. Адлеман заказал достаточное количество материала для исследования сети из 7 городов, а затем просто разложил нити по пробиркам. Нити принялись за параллельную обработку информации: они начали соединяться, создавая множество разных маршрутов обхода сети. Разумеется, многие из этих маршрутов нарушали правило, запрещающее посещать города больше одного раза. Но Адлеман понимал, что тот маршрут, который он ищет, должен представлять собой нить ДНК, длина которой равна
8 (город отправления) + 6 × 8 (для каждой дороги) + 8 (город назначения).
Для отбора таких нитей и проверки присутствия в их последовательностях всех городов годилась процедура, сходная с генетической дактилоскопией.
Хотя весь этот процесс занял больше недели, он открыл интересные перспективы: возможность использования биологических структур для создания машин, способных эффективно производить параллельную обработку информации. Для измерения количества молекул в пробирке химики используют единицу под названием «моль». Но один моль вещества содержит чуть более 6 × 1023 молекул
[134]. Адлеман считает, что использование предельно малых биологических объектов может стать шорткатом к решению предельно больших вычислительных задач.
Не исключено, что природа уже преуспела в этом. Оказывается, один странный организм, относящийся к классу собственно слизевики, довольно хорошо умеет находить самые рациональные маршруты передвижения по карте. Это слизевик Physarum polycephalum, который представляет собой плазмодиевый одноклеточный организм, растущий вовне из исходной точки в поисках источников пищи. Его любимая еда – овсяные хлопья.
Группа исследователей из Оксфорда и Саппоро решила задать своему слизевику следующую задачу: найти кратчайший маршрут среди овсяных хлопьев, разложенных так же, как расположены станции железнодорожной сети Токио и его окрестностей. У инженеров ушли целые годы на разработку наиболее рациональной схемы соединения городов. А на что способен слизевик?
Изначально слизевик ничего не знает о местах расположения хлопьев и начинает расти во всех направлениях. Но, когда он начинает натыкаться на источники пищи, многочисленные отростки, которые пищи не нашли, отмирают, и остаются только наиболее удобные соединения с источниками пищи. Всего за несколько часов слизевик настраивает свою структуру, создавая между новыми источниками пищи соединения, удобные для достижения разных точек.
Экспериментаторов поразил тот факт, что получившаяся структура слизевика была очень похожа на схему железнодорожных сообщений, созданных людьми в окрестностях Токио. У людей на это ушли многие годы. Слизевик справился за несколько часов. Неужели это одноклеточное существо знает шорткат, который сможет помочь нам решить одну из величайших нерешенных задач математики?



