
Деление по модулю – это обычное деление целых чисел друг на друга с целым остатком. Подобную арифметическую операцию проходят в младших классах школы, непосредственно перед изучением дробей. После чего про деление с остатком благополучно забывают и не вспоминают до университетского курса высшей математики. Где неожиданно выясняется, что деление с остатком на самом деле играет довольно важную роль в теории чисел и алгебре. В нашем примере мы должны определить, в какую степень нам надо возвести тройку, чтобы потом, разделив полученный результат по модулю на 17, получить число 13 в качестве остатка от деления. Правильный ответ: x = 4. То есть 34 = 81, 81/17 = 4 + остаток 13 (проверка: 4 x 17 = 68 + 13 = 81). Довольно просто, не правда ли? Возводя тройку в различные степени x от единицы и более, а затем деля по модулю полученный результат на 17, мы будем каждый раз получать различные остатки от деления. Однако у них будет одно общее свойство – все эти остатки будут находиться в диапазоне от 1 до 16 включительно, но выстраиваться отнюдь не по порядку (по мере последовательного возрастания степени x). Множество этих чисел называется кольцом вычетов. Кольцом, потому что остатки будут постоянно повторяться для разных показателей степени, в которую возводится базовое число. А теперь представим, что мы оперируем не одно-двухразрядными, а очень большими числами. В этих случаях, если степень заданного числа нам заранее неизвестна, то задача ее нахождения для конкретных величин остатков становится очень и очень сложной. Именно эта сложность и лежит в основе алгоритма DSA.
Как уже упоминалось выше, все подобные алгоритмы шифрования построены на принципе, при котором задача в одну сторону решается очень быстро и просто, а в обратную – исключительно сложно. И алгоритм DSA – не исключение. Если мы будем решать задачу для больших чисел путем простого перебора различных значений, то данный метод будет работать очень медленно. Поэтому вместо обычного перебора были разработаны алгоритмы, которые решают эту задачу гораздо эффективнее. Настолько эффективно, что, принимая во внимание постоянное увеличение производительности современных компьютеров, математики вынуждены были задуматься о необходимости повышения сложности алгоритма шифрования. В противном случае они могли бы столкнуться с проблемой массового взлома шифров уже в относительно недалеком будущем.
Чтобы придать задаче существенное усложнение, в 1985 году был разработан алгоритм дискретного логарифмирования на базе эллиптических кривых (алгоритм ECDSA). О чем в данном случае идет речь и что это за кривая? Эллиптическая кривая – это множество точек, описываемое уравнением y2 = x3 + ax + b. То есть, по сравнению с алгоритмом DSA, операции совершаются не над кольцом целых чисел, а над множеством точек эллиптической кривой, что существенно усложняет задачу восстановления закрытого ключа из открытого. Вот пример обычной эллиптической кривой:
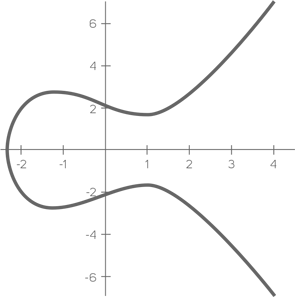
На множестве точек эллиптической кривой могут выбираться такие точки, для которых возможно совершить операцию сложения самих с собой и получить результат в виде другой точки на этой же кривой. То есть решить уравнение X = nP, где n = 2 и более, а X и P являются точками на данной кривой с координатами по осям x и y. Умножение на константу n есть не что иное, как операция последовательного сложения n раз. Таким образом, мы начинаем с того, что нам необходимо сложить начальную точку с ней же самой и получить результат в виде такой же точки, но уже с новыми координатами. Геометрически операция сложения точки эллиптической кривой с самой собой представляет построение касательной к данной точке. Затем мы находим точку пересечения касательной с графиком кривой и строим от нее вертикальную прямую, находя таким образом точку ее пересечения на обратной стороне кривой. Эта точка и будет результатом сложения. Вот как выглядит операция сложения точки с самой собой геометрически:
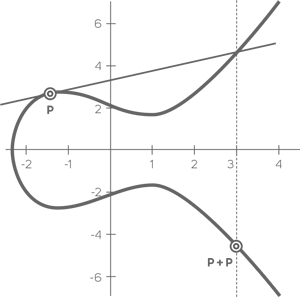
После чего, уже при следующей итерации, исходной точкой будет являться та, которая была получена в виде результата сложения на предыдущем шаге. Именно от нее мы строим новую касательную, и так далее – n раз. Сложность задачи состоит в обратном поиске n для известных точек X и P, и эта задача не имеет быстрого решения. В данном случае n будет закрытым ключом, а X – открытым. Понятно, что компьютер при расчетах осуществляет операцию сложения не геометрически, а чисто алгебраически, для чего существуют специальные формулы на базе имеющихся координат по осям x и y для каждой из точек.
Отдельно отметим, что далеко не все формы эллиптических кривых подойдут для формирования на их базе криптографических алгоритмов. Существуют довольно «слабые» в этом аспекте эллиптические кривые, которые неустойчивы к различным алгоритмам решения задачи дискретного логарифмирования. Поэтому, чтобы эллиптическая кривая была пригодна для сложных криптографических задач, она должна удовлетворять различным требованиям, которые мы здесь рассматривать не будем, чтобы излишне не усложнять описание общих принципов.
В теории алгоритмов выделяют различные категории сложности решения математических задач: полиномиальную, субэкспоненциальную и экспоненциальную. Сложность алгоритма дискретного логарифмирования на базе эллиптических кривых растет с экспоненциальной скоростью. До сих пор не разработано ни одного решения данной задачи даже за субэскпоненциальное время. То есть за время, пропорциональное функции, которая растет медленнее, чем любая степенная функция. Именно поэтому данный алгоритм получил в наши дни наиболее широкое применение как достаточно криптостойкая модель, использующая ключи с относительно небольшой разрядностью. Если мы сравним вышеописанные алгоритмы между собой, то для случая, когда длина открытого ключа RSA или обычного DSA, например, будет равна 1024 бит, алгоритму, использующему эллиптические кривые для достижения сопоставимой криптостойкости, достаточно будет иметь разрядность всего 160 бит. Разница в эффективности очевидна, поэтому самые популярные блокчейн-проекты, такие как Биткоин или Ethereum (да и многие другие), используют именно криптографию на эллиптических кривых, признанную на текущий момент самой надежной.
Помимо собственно процедуры шифрования данных важнейшим элементом, связанным с шифрованием, в технологии блокчейн является цифровая электронная подпись (ЭЦП). Что это такое и каким образом она используется?
Цифровая электронная подпись
Привычное для нас понятие «подпись» старо как мир – задача проверки подлинности документов стояла перед человечеством с древнейших времен. В качестве элементов, усложняющих подделку документов, использовались уникальные формы начертания имени чиновника, купца, феодала или даже монарха, созданные рукой самого автора. Делалось это подчас в сочетании с сургучными или восковыми печатями с оттиском государственных или родовых гербов подписанта. Считалось, что данная комбинация в большой степени защищает документ от несанкционированного воспроизведения с измененными в пользу фальсификатора данными. В большинстве случаев эти защитные меры действительно себя оправдывали. Однако не существовало никакой гарантии, что какой-нибудь средневековый злоумышленник, вооруженный специальными для таких случаев приспособлениями, не сможет воссоздать копию документа, достаточно близкую к оригиналу.

