Следующий алгоритм, который также считается постквантовым, – это так называемая «криптография на решетках». Решеткой в математике называют периодическую сеть точек в n-мерной системе координат, где задано число n «базисных векторов», порождающих саму решетку. Вот простой пример решетки для прямоугольной системы координат с двумя заданными базисными векторами.
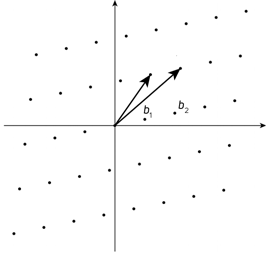
Сложная для вычисления задача в данном алгоритме – это нахождение так называемого SVP (Shortest Vector Problem) или «наиболее короткого вектора» для заданных базисных векторов при условии существенного увеличения размерности пространства n. Если рассматривать обыкновенную плоскую двумерную решетку, то найти глазами точку, наиболее близкую к заданному узлу решетки, для человека не составляет никакого труда. Однако если это будет делать компьютер, то в ход пойдут непростые математические вычисления. А если начать увеличивать количество пространственных измерений, то процесс превратится в весьма серьезную вычислительную задачу. Считается, что на данный момент сложность такой задачи превышает возможности квантового компьютера. Впрочем, из алгоритмов, базирующихся на криптографии на решетках, неуязвимым пока признается только непосредственно само шифрование. Цифровая электронная подпись уже подверглась взлому в 1999 году, а ее модифицированная версия – в 2006 году. В настоящее время математики работают над дальнейшим развитием алгоритма ЭЦП, чтобы разрешить эту проблему и предложить индустрии новый, более совершенный стандарт криптографической безопасности.
Наконец, рассмотрим, возможно, самый перспективный на текущий момент алгоритм – использование криптографии на базе изогений эллиптических кривых. Изогения – это метод, позволяющий отобразить точку, принадлежащую одной эллиптической кривой, в точку на другой кривой подобного же типа. Алгоритм преобразования точек представляет собой соотношение двух полиномов (многочленов) для каждой из координат точки по осям x и y. В случае если получить такое отображение считается математически возможным, то эти две кривые будут являться изогенными по отношению друг к другу. Для каждой из кривой можно рассчитать так называемый «j-инвариант», являющийся чем-то вроде «классификатора» эллиптической кривой и представленный в виде обычного числа. Для расчета j-инварианта используются коэффициенты из уравнения эллиптической кривой. Применяя различные значения коэффициентов, рассчитывают множество инвариантов, которые затем отображаются в виде графа. В полученном графе инварианты становятся его вершинами, а ребрами графа служат соединения тех инвариантов, эллиптические кривые которых изогенны друг другу. Собственно, нахождение путей в графе между вершинами или, другими словами, вычисление изогении между различными эллиптическими кривыми и есть та сложновычислимая задача, на базе которой строится данный криптографический алгоритм. Структуры, построенные на основе последовательно наложенных друг на друга графов эллиптических кривых, представляют собой очень красивые геометрические объекты, как, например, сложная «звезда изогений», показанная на рисунке:
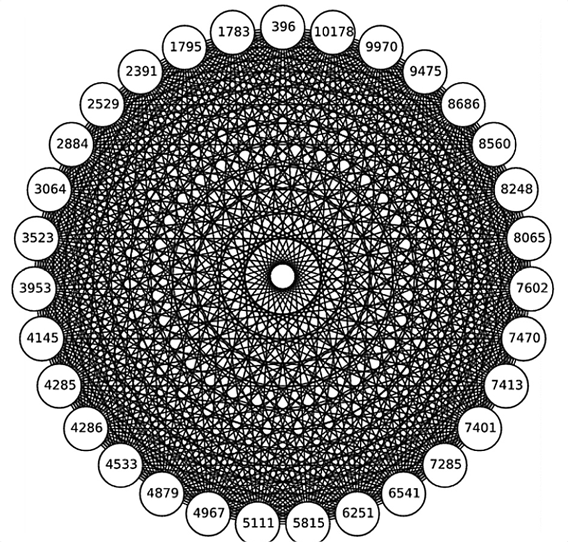
Очевидно, что применение изогений существенно усложняет эллиптическую криптографию. Если в классическом варианте мы имеем дело только с одной эллиптической кривой, то в случае с изогениями – с целым их «семейством», что возводит решение задачи в дополнительную степень сложности. Даже квантовому компьютеру не под силу решить эту задачу за субэкспоненциальное время, что говорит об исключительной криптостойкости алгоритма, который с полной уверенностью можно считать «постквантовым». Скорее всего, данный алгоритм на текущий момент является наиболее пригодным для построения на его основе блокчейн-проектов, которые стремятся обеспечить максимальную безопасность данных для своих пользователей. А в свете активно развивающейся индустрии квантовых вычислений эта проблема становится действительно актуальной.
Теория игр и блокчейн
Когда мы рассматривали децентрализацию как способ управления, была обозначена проблематика сложности взаимодействия равных по правам субъектов в системах, где консолидирующий и управляющий центр отсутствует как класс. И ведь действительно, каким же наиболее эффективным образом равноправным участникам системы следует приходить к единым решениям, которые устроят если не абсолютно всех, то подавляющее большинство? Очевидно, должна существовать некая процедурно обусловленная форма общественного согласия, позволяющая принимать решения, обязательные к исполнению всем сообществом. При этом она не должна создавать неразрешимые конфликты, ведущие к разрушению системы в целом. Этот комплекс мер называется формированием правил для прихода к консенсусу, то есть единодушия во мнениях между заинтересованными лицами при принятии важных для системы решений без затратной, с точки зрения ресурсов, процедуры прямого голосования.
Совокупность стремлений участников системы извлечь собственную или общественную выгоду, преодолевая при этом явное или скрытое сопротивление других участников с противоположными интересами, можно описать словом «игра». Разумеется, для реализации своих целей каждый из участников оперирует той или иной специально разработанной стратегией, которая стремится к достижению максимального эффекта в решении поставленных задач. В математике существует специальный раздел, посвященный изучению оптимальных стратегий в играх. Он так и называется – «теория игр», и мы рассмотрим ее отдельные элементы, поскольку они являются важным звеном при построении блокчейн-систем, которые почти всегда децентрализованы, а ее участники равноправны. Речь идет в первую очередь о методах формирования консенсуса между узлами сети при создании цепочки блоков, а также наборов транзакций в них. Но об этом чуть позднее. Сначала попробуем уяснить для себя, что же является эффективной или неэффективной стратегией при достижении общего согласия.
Эффективность стратегии неразрывно связана с понятием рационального поведения участников. Чтобы убедиться, что сотрудничество между участниками «игры» не всегда гарантировано, даже если это сообразуется с их общими интересами, рассмотрим известную «Дилемму заключенного». Она была представлена в 1950 году американскими математиками Мерилом Фладом и Мелвином Дрешером. В тюрьму почти одновременно и за одно и то же деяние попадают двое преступников. Небезосновательно предполагая возможный сговор между ними, полиция изолирует их друг от друга, а затем предлагает каждому одинаковые условия сотрудничества со следствием. Форма сотрудничества предполагает свидетельство одним заключенным против другого в обмен на немедленное освобождение. Также предполагается, что, если второй заключенный на сотрудничество с полицией не идет, он получает максимальный тюремный срок. В случае если оба отказываются сотрудничать, каждый получает минимальный срок. Если же имеет место взаимное обличение, то оба получают средний по длительности срок. Понятно, что, находясь в изоляции, заключенные не знают о решении друг друга. Какова же тогда в этом случае наиболее эффективная стратегия для каждого из заключенных?

