Но… Эйнштейн ли это?
Это во многом зависит от того, как далеко вы находитесь от рисунка. Держа его на расстоянии вытянутой руки, как, вероятнее всего, вы делаете это прямо сейчас, вы не совсем понимаете, о чем я говорю. Но посмотрите на тот же снимок с другого конца комнаты, и вы, как и большинство людей, сразу же поймете, о чем я.
То, что мы видим, во многом зависит от того, как мы глядим. По мнению большинства психологов и закоренелых психофизиков, это основополагающий принцип человеческого восприятия.
Иллюзия работает, потому что существует значительный дисбаланс в уровне пикселизации между двумя соответствующими изображениями, составляющими его. Изображение Мэрилин Монро состоит из значительно меньшего количества пикселей, чем изображение Альберта Эйнштейна, поэтому его можно распознать только на расстоянии. Другими словами, на более близком расстоянии Альберт подавляет Мэрилин, что позволяет мельчайшим деталям его внешности, например, прядям его волос и усам, бросаться наблюдателю в глаза.
Время тоже играет роль. Исследователи из Массачусетского технологического института, создавшие это изображение, показывали его людям в своей лаборатории в течение разных интервалов времени, спрашивая их, что они видели. Появилась четкая закономерность. Те, кто видел изображение в течение более короткого промежутка времени (30 миллисекунд), видели Мэрилин и ничего больше. Напротив, те, кому показывали изображение в течение 150 миллисекунд, смогли распознать Альберта.
Когда времени мало, мы видим мир черно-белым. Наш мозг составляет общую картину, упуская детали, потому что раньше такой механизм позволял человеку выжить. Но при приближении иллюзия рассеивается, и Альберт Энштейн сменяет Мэрилин Монро.
Глава 6
Сложность простоты
Найдите время, чтобы подумать, но, когда пришло время действовать, не думайте и идите вперед.
Наполеон Бонапарт
Когда я изучал прикладную математику в школе, учитель предложил нам решить задачу, которая теперь широко известна благодаря Google. Ее придумал француз-математик Клод-Гаспар Баше де Мезириак, и она упоминается в его рукописи 1624 года.
Помощник торговца специями однажды ехал по дороге на своей повозке, но вдруг резко притормозил, чтобы избежать столкновения с другой. Повозка остановилась, но 40-килограммовый груз, который был в ней, упал на землю и развалился на четыре части. Помощник торговца расстроился и разозлился. Несмотря на то, что авария произошла не по его вине, торговец потребует с него компенсацию и вычтет деньги из его заработной платы.
Но внезапно у мужчины возникла идея (так как он, наверно, гений математики). Идея, которая прекрасно иллюстрирует концепцию оптимальной категоризации, о которой мы размышляли недавно: разумное разделение разрозненного и разнообразного мира на различное число функционально «оптимальных» категорий в зависимости от контекста и потребностей текущей ситуации. При взвешивании четырех раздробленных фрагментов своего груза весом 40 килограммов помощник быстро определил, что с помощью этих фрагментов и весов с чашами он может определить вес любого груза от 1 килограмма до 40 килограммов.
Вопрос: каков вес каждого из четырех фрагментов?
Сейчас существует исчерпывающее математическое доказательство решения задачи Баше, но я не буду останавливаться на нем и скажу, что фрагменты весили 1, 3, 9 и 27 килограммов.
По замыслу Баше, груз можно взвесить, расположив фрагменты 40-килограммового груза на обеих чашах весов. Фрагмент, который помещают на чащу с грузом, приобретает отрицательный вес.
Представим, что нам нужно получить определенное количество специй. Вот как фрагменты груза в этом помогут.
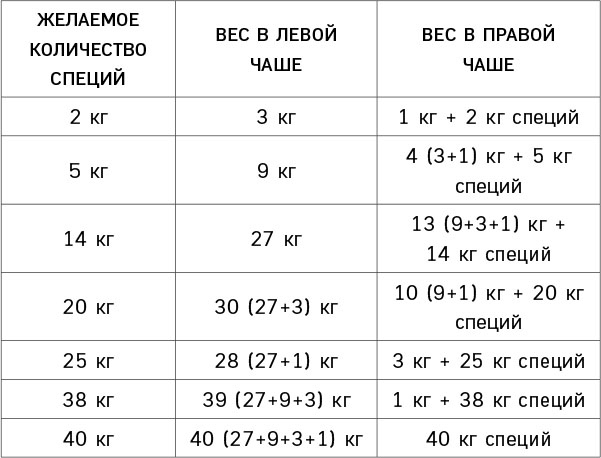
Задачу Баше очень любят учителя математики в старших классах. Чтобы ее решить, не нужно быть Хокингом или Эйнштейном: просто нужно хорошо знать методы алгебраических вычеслений и основы логического мышления.
Например, чтобы отмерить 2 килограмма специй, вы можете сразу использовать гирю весом 2 килограмма. С другой стороны, гирями весом в 1 и 3 килограмма можно измерить любой вес до 4 килограммов, что куда удобнее.
Но задача Баше – это еще и элегантная иллюстрация дилеммы, с которой веками сталкивались информационные архитекторы, в том числе те, кто разрабатывает новые валюты. Как придумать минимальный номинал монеты и банкноты и их комбинаций, чтобы обеспечить наиболее эффективное использование денег?
Учитывая ответ на загадку Баше, можно было бы предположить, что нужно использовать число 3 в разных степенях (1, 3, 9, 27 или 30, 31, 32, 33). В Великобритании, например, было бы тогда 1, 3, 9, 27, 81 пенни. Или £1, £3, £9, £27, £81. Но есть проблема: практически все валюты в наши дни десятичны, и поэтому структурно несовместимы с исходной структурой Баше. Любой центральный банк, который начинает возиться со своими нулями, будет играть с фискальным огнем. Кроме того, не факт, что задача со степенями – это то, с чем хочет столкнуться человек в очереди в баре в пятницу вечером.
Экономисты в различных странах нашли альтернативное решение и стали использовать числа 1, 2 и 5. Это ряд предпочтительных чисел, то есть последовательность чисел, которые можно умножить на степень удобного основания, обычно 10, для стандартизации, упрощения и максимизации совместимости между объектами, сущностями и точками данных в широком разнообразии контекстов. Денежные знаки являются, пожалуй, наиболее яркими примерами.
1, 2, 5, 10, 20, 50 пенни.
£1, £2, £5, £10, £20, £50, £100.
Как вы могли заметить, ряд чисел 1, 2 и 5 недалеко отошел от последовательности Баше. Единственное отличие между ними в том, что если в ряду Баше соотношение между соседними целыми числами составляет 1:3, то в ряду 1, 2, 5 оно равно 1:2 или 1:2,5. С точки зрения экономики это означает, что любой номинал валюты должен быть в два или два с половиной раза больше предыдущего. Эта экономическая модель способствует простоте, удобству и точности повседневных транзакций. Зайдите в магазин с купюрой 10 фунтов и купите что-нибудь за 3 фунта, сдача должна быть в виде купюры 5 фунтов и монеты в 2 фунта. Не 14 монет по 50 пенни. Или семь монет по 1 фунту. Или три монеты по 2 фунта и одна монета в 1 фунт. Хотя все мы с этим сталкивались.
Ряд чисел 1, 2, 5 доказывает, что упростить можно все что угодно, было бы желание. Но, как и задача Баше, он указывает на фундаментальную загадку, с которой каждый из нас сталкивается в повседневной жизни. Как мы видели из предыдущих глав, проблема оптимальной категоризации касается всех нас. Но в повседневной жизни решения не всегда можно принять с легкостью, с которой весы отмеряют специи.

